Relativité

Rappelons que la température d'un gaz (ce qu'il y a de plus simple à définir) dit parfait (pas d'interaction entre les particules) est reliée à son énergie cinétique.

Une particule de masse m ayant une vitesse v présente une énergie cinétique :

La loi de distribution des vitesses de Maxwell (théorie cinétique des gaz) relie la vitesse quadratique moyenne v² de N particules et la température via la constante de Boltzmann :

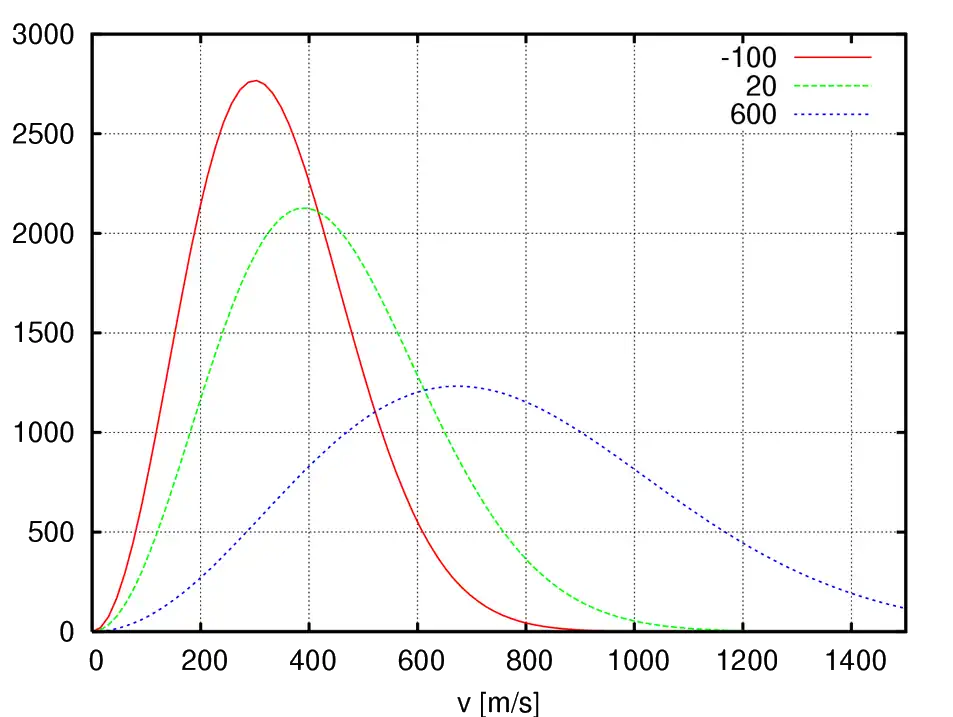
Attention, il s'agit d'une distribution de vitesses, et la vitesse la plus probable n'est pas la vitesse quadratique moyenne :

Du coup on peut indiquer une vitesse pour donner une température connaissant la masse de la particule, dans l'exemple ci-dessus :

• −100°C : 367 m/s
• 20°C : 478 m/s
• 600°C : 825 m/s

Vous avez compris que la chaleur relativiste n'est certainement pas à propos de la vitesse des particules d'un gaz.

Ceci dit, il existe une théorie de gaz parfait relativiste, ou thermodynamique relativiste ça claque dans une conversation avec des particules présentant une vitesse proche de la lumière. Qui est d'un intérêt très relatif. À part pour les étoiles très chaudes ou la fusion nucléaire. Et encore.

Soit deux référentiels en mouvement l'un par rapport à l'autre, celui où Alice est fixe, et celui où Bob est fixe.

La théorie de la relativité restreinte permet à Alice de calculer ce qui passe pour Bob qui est en mouvement, sur les aspects spatio-temporels = pour le temps et les longueurs. Autrement dit, elle donne les formules de changement de référentiel, que voici :

Transformation de Lorentz pour passer du référentiel Alice au référentiel Bob se déplaçant à la vitesse v le long de l'axe des x, avec β = v/c, et le facteur de Lorentz γ :

│ ct' = γ ( ct - β x )
│  x' = γ (  x - β ct )
│  y' = y
│  z' = z

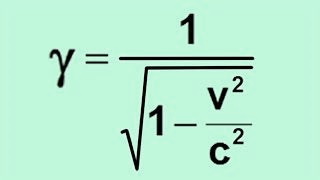
Il se passe deux choses :

1. Le temps ne s'écoule pas de la même manière chez Bob et Alice, il existe une histoire de dilatation du temps.

   C'est une expression confusante car on se demande toujours dans quel sens ça marche, quelle est la pendule qui retarde.

2. Les longueurs mesurées entre Alice et Bob du même objet ne sont pas les mêmes, ce sont les histoires de contraction des longueurs.

   C'est l'inverse du temps, forcément, faut bien que ça se compense quelque part.

   Remarquez qu'une longueur, ce n'est jamais qu'un temps si on utilise la vitesse de la lumière comme étalon.

Le rapport est donné par le facteur de Lorentz γ, c'est pour ça qu'il est si important. Le facteur de Lorentz γ est toujours supérieur à 1.

En ce qui concerne l'énergie le facteur de Lorentz s'applique également :

L'énergie augmente dans le référentiel en mouvement. Cela deviendra important quand il faudra conserver l'énergie en injectant de la chaleur.

Alice est tranquillement dans sa station spatiale, dont la température est stabilisée à une température confortable, par exemple 24°C.

Bob passe non loin de la station avec son vaisseau spatial déboulant à 80% de la vitesse de la lumière. Pour Bob, quelle est la température qu'il mesurerait (s'il pouvait le faire) ?

Avant de tenter de calculer la température lue par Bob, on peut se demander comment mesurer la température en pratique depuis un vaisseau spatial, ou une planète qui se déplacerait à une vitesse relativiste par rapport à Alice.

On peut raisonnablement se demander quel signal, probablement électromagnétique, partirait de chez Alice pour parvenir à Bob, avec un certain temps, ce qui rendra le résultat d'un intérêt relatif...

De toutes manières, obtenir une température "apparente" est de peu d'intérêt.

Il est peut-être plus simple que Bob envoie une sonde de température, qui, une fois parvenue sur place, effectuera la mesure localement, puis retournera le résultat par un moyen quelconque, par retour de la sonde ou électromagnétiquement.

À ce moment-là, on obtiendra la température qu'aurait lue Alice, dans un référentiel fixe. D'ailleurs, si Alice est disponible, autant lui passer un coup de fil pour lui demander la température...

Mais bon, du point de vue intellectuel, il est intéressant de calculer ce que verrait Bob, surtout si Alice n'est pas là, et ainsi Bob pourra appliquer la correction adéquate pour obtenir la température propre.

Eh bien ce fut compliqué pour tout le monde, Einstein et Planck dans les premiers. Il existe trois cas lorsque l'on lit la température dans le référentiel en mouvement :

• La température est la même. Très vite abandonnée. Que l'entropie soit invariante (processus réversible), cela parait normal, et comme la quantité de chaleur c'est la température multipliée par l'entropie, ça pose bien trop d'ennuis...
• La température augmente. C'est ce que pense Einstein et Planck. Au repos, on a la température la plus basse possible.
• La température diminue.

Lorsqu'il existe une variation, c'est le facteur de Lorentz qui intervient (plutôt son inverse qu'on voit dans les équations).

Eh bien la controverse existe encore, sauf qu'il semble bien que la température lue augmente, nous allons survoler plusieurs démonstrations pour montrer cela.

Voici un résumé des arguments qui vont dans le sens où la température d'un corps est la plus haute dans son référentiel propre, lorsque l'on lit la température dans un autre référentiel, c'est la même ou alors elle est plus basse.

On pourra lire le détail dans ce papier :

• Expression relativiste de la chaleur.pdf / Laurent SCHOEFFEL

C'est probablement le plus simple et évident : traiter la chaleur au niveau de l'énergie du système.

Dans le référentiel au repos, pour se simplifier les choses, supposons au départ que le corps C est au zéro absolu = pas de chaleur. Son énergie est donnée par sa masse avec la célèbre formule :

Et son énergie dans le référentiel en mouvement est :

Plaçons une source de chaleur près du corps C qui va donner une quantité de chaleur Q, donc de l'énergie, dans le référentiel au repos :

Dans le référentiel en mouvement, comment voit-on les choses ? Une variation d'énergie se traduit par une variation de la masse propre :

C'est comme si on avait ajouté une masse propre, c'est l'équivalence de la masse et de l'énergie.

Mais si a ajouté une masse propre Δm (sous forme de chaleur, une énergie donc une masse), il aura fallu fournir un travail W' provenant d'une force F à cet ajout pour conserver la vitesse globale W'=∫Fvdt. La relation fondamentale de la dynamique nous donne la quantité de mouvement (relativiste) :

Notez que ce travail n'arrive pas dans le référentiel au repos puisque tout est au repos.

Dans le référentiel en mouvement, l'énergie augmente du travail W' et d'une quantité de chaleur Q' "relativiste" qu'on aimerait connaitre pour arriver à la température :

On arrive alors à extraire la chaleur Q' en éliminant le travail W' :

Or on connait Δmc² dans le référentiel au repos, il s'agit de la quantité de chaleur Q, la variation de masse propre, et on obtient simplement :

Et comme la quantité de chaleur et la température sont reliées par l'entropie S qui est un invariant relativiste S=Q/T, on a exactement la même chose pour la température :

La température du référentiel propre est toujours la plus haute, la plus grande. Comme le temps du reste...

On peut tenter de calculer la vitesse quadratique moyenne vue dans le référentiel en mouvement, ce qui nous permettrait de connaitre la température de ce point de vue. C'est en fait plus simple qu'il n'y parait car on peut appliquer un raisonnement à la limite, quand la vitesse du référentiel en mouvement tend vers la vitesse de la lumière.

Une molécule est animée d'une certaine vitesse dans le référentiel au repos. Dans le référentiel en mouvement à la vitesse v le long de l'axe des x, les vitesses deviennent (c'est pareil pour y et z) :

L'élément important ici est ce qui se passe quand on augmente (inconsidérément) la vitesse v du référentiel en mouvement. Lorsque v tend vers c, alors le facteur de Lorentz γ tend vers l'infini, et les vitesses "transverses" en y et z tendent vers zéro. Et en plus, la vitesse en x tend vers c.

Autrement dit, vu dans le référentiel en mouvement, les molécules finissent par se déplacer dans un bel ensemble toutes dans la même direction, le désordre tend à disparaitre, ce qui est très gênant pour la chaleur !

Il existe également une démonstration basée sur la statistique d'un gaz parfait, où on retrouve au premier ordre le résultat précédent. Regardez le document donné en référence si vous voulez creuser.

Dans le résultat obtenu, on objecte que la quantité de chaleur qui a été transférée possédait déjà elle-même une impulsion propre. Et donc le travail W qui a été introduit n'est pas requis, ce qui modifie notablement le résultat.

Les opposants font aussi remarquer que le radiateur qui donne la chaleur est en contact avec le corps C, et le reste. Alors que l'on ajoute une impulsion au corps C avec le travail W, ce qui devrait le séparer ! Ceci montre qu'il n'existe pas de travail fourni, il n'y a que de la chaleur échangée.

Si vous vous posez la question, c'est que vous êtes largué, la gravitation n'a rien à voir avec tout ça.