Relativité
10 mai 2024

La contraction des longueurs de la relativité restreinte fait souvent croire que les objets maigrissent dans la direction du déplacement, ce qui est vrai si on effectue une mesure, mais faux si on les regarde visuellement. Et c'est plus compliqué que ça, pour un résultat surprenant : on observe une rotation dite de Terrell.

Contraction des longueurs

😯 Alors comme ça les longueurs se contracte lorsque les objets se déplacent rapidement ?
😬 Euh, pas tout à fait.
Cela dépend de la vitesse par rapport à l'observateur.
Des observateurs différents, à des vitesses différentes, verront des contractions différentes.
Ce que raconte la relativité spéciale...
Restreinte. 🤓 En français on dit relativité restreinte.
Ces sont les roosbeefs qui disent special relativity.
😐 Oui, bon, d'accord.

Transformation de Lorentz pour passer du référentiel Alice au référentiel Bob se déplaçant à la vitesse v le long de l'axe des x :

│ ct' = γ ( ct - β x )
│  x' = γ (  x - β ct )
│  y' = y
│  z' = z

Avec β = v/c, et le facteur de Lorentz γ :

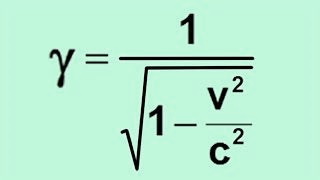
facteur de Lorentz
Ce que raconte la relativité restreinte est donc vrai ?
Bien sûr. C'est un observateur immobile qui aura la plus grande longueur lors de la mesure.
C'est pour ça qu'on parle de contraction des longueurs.

Le vaisseau de Bob est plus long au repos que lorsqu'il est vu en mouvement par Alice. Le mouvement provoque une contraction des longueurs.

Transformation de Lorentz pour passer du référentiel Alice au référentiel Bob se déplaçant à la vitesse v le long de l'axe des x (y et z sont inchangés) :

En plaçant une extrémité du vaisseau de Bob en 0 à t=t'=0 dans le référentiel de Bob, elle est aussi en 0 dans le référentiel d'Alice.
L'autre bout est à LBob(vaisseau) pour Bob, et LAlice(vaisseau) pour Alice.
La seconde équation de la transformation de Lorentz lie les deux longueurs :

LBob(vaisseau)  = γ LAlice(vaisseau)

Autrement dit le vaisseau de Bob est plus court pour Alice. Si le vaisseau spatial de Bob faisait 1000 m, alors pour Alice il ne fait plus que 1000/1.666 = 625 m à 80% de la vitesse de la lumière. Mais uniquement dans l'axe du déplacement, il est aplati.

On peut le représenter graphiquement facilement :

Alice et Bob, chacun de leur côté.
Alice: "Eh Bob! T'aurai pas maigri un peu ? Tourne-toi pour voir..."
attention: il s'agit d'une mesure, pas ce qu'on voit...
😧 Et quand l'observateur se déplace vite, il voit l'objet plus court ?
🧐 Attention, qu'est-ce que t'entend par "voir" ? Tu effectues une mesure ou tu le regardes avec tes yeux ?
🤔 C'est différent ?
😏 Un peu, mon neveu !
Parce que la lumière qui arrive de deux endroits différents n'a pas forcément suivi le même parcours spatio-temporel...

On ne voit aucune contraction

Qu'est-ce qu'on voit alors ?
Eh bien tu verras l'objet plus ou moins sous sa forme normale, ce qui parait contradictoire

Quelques références d'où j'ai tiré les images (que j'ai corrigées) :

Voici l'exemple simple d'un cube que l'on va observer.

Un cube va être observé.

L'observateur est loin devant la taille du cube, aussi les rayons de lumière sont considérés parallèles. Le côté du cube est de longueur L, au repos.

Si le cube bouge doucement, on verra (bêtement) la face du cube.

Pour commencer, on va tourner un peu le cube, d'un angle θ, mais il se déplace toujours doucement. On observe alors deux faces, chacune d'une taille dépendant de l'angle de rotation.

Le cube est un peu tourné, rien de spécial, on voit deux faces. On voit qu'il a tourné un peu.

Sans relativité restreinte / sans contraction

Reprenons notre cube sans rotation. S'il se déplace à une fraction de la vitesse de la lumière, mais que l'on néglige la théorie de la relativité restreinte, il n'existe aucune contraction.

Sans histoire de relativité, pas de contraction, même si le cube se déplace vite.

MAIS la vitesse de la lumière est finie, aussi, pour que tous les photons arrivent au même instant à l'œil de l'observateur, il aura fallu que les photons provenant du coin E partent un poil plus tôt !

Il faut un temps L/c pour que le photon partant de E arrive en B. Et pendant ce temps-là, le cube se déplace de L.v/c. Une face du cube apparait, alors qu'il n'est même pas tourné ! Et ça n'a rien à voir avec la relativité restreinte.

Vu du cube se déplaçant à la vitesse v, SANS contraction liée à la relativité.
Notez que l'on voit une face du cube, alors qu'il est face à nous, SANS rotation...
😦 Ah tiens ! Il semble avoir tourné !
Pas tout à fait, les dimensions ne collent pas tout à fait avec une rotation.
😒 Mouais, effectivement. On voit un côté qu'on ne voyait pas avant.
🤓 Et ça, sans effet bizarre lié à la relativité restreinte.
C'est juste que la vitesse de la lumière n'est pas infinie.

Inclusion de la relativité restreinte / avec contraction

Si on prend en compte la contraction liée à la relativité restreinte, voilà ce que ça donne :

Seul le segment AD est raccourci, rien dans les autres directions

Le cube apparait comme s'il avait réalisé une rotation de cos θ = 1/γ !

Regardez le cube tourné à vitesse lente que l'on a vu juste avant...

😲 Whoah !
Le cube apparait avoir subi une rotation, dite de Terrell.

C'est un Autrichien, Anton Lampa, qui l'a exhibé en 1924, redécouvert par James Terrell en 1959, ainsi que par Roger Penrose, d'où le nom complet de l'effet.

Voici l'effet transposé à un cycliste, comme l'a proposé Gamov
A vitesse normale
😏 On dirait Einstein
Lancé à 93% de la vitesse de la lumière, si on le mesure, il s'aplatit
Tel que l'a décrit Gamov, sauf que c'est trompeur, ce n'est pas ce que l'on voit.
Il est tout maigre, c'est la contraction des longueurs dans la direction du déplacement
Effectivement, mais ce n'est pas ce que l'on verrait !
Photographier n'est pas mesurer
😯 Ah oui, on dirait qu'il a tourné et qu'il s'éloigne.
Sauf que ce n'est pas le cas, il est juste devant toi en train de traverser !
😐 Et il a une taille à peu près normale !
🤓 Penrose a montré qu'une sphère ... restait une sphère.
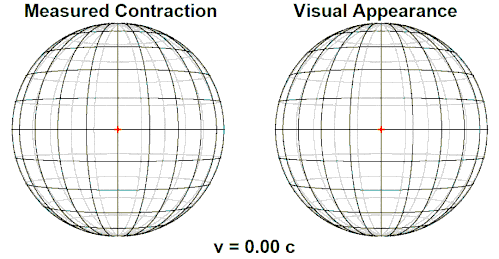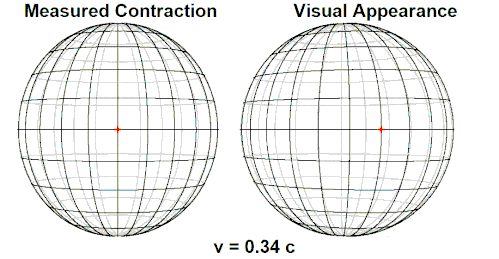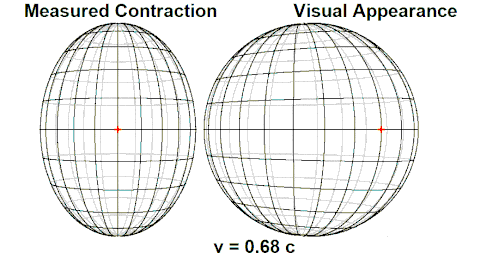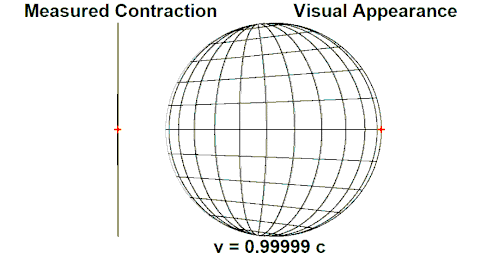
sphere relativiste
Une sphère reste sphérique à vitesse relativiste, aussi surprenant que cela paraisse. Mais elle tourne.
Voilà qui sera commode pour les voyages interstellaires, au moins les planètes auront toujours une tête de planète.

Le train entre en gare

Au fait, quand on s'approche avec un angle, c'est pareil ?
Ben il faut se peler le calcul.
Vous trouverez dans les références un lien avec les calculs
Je te fais grâce des calculs, voici une animation parlante.
C'est une illusion, le dé ne tourne pas !

Voici une description vidéo, ma foi intéressante, de ce qui se passe si on voyage à des vitesses folles. La rotation de Terrell y est brièvement décrite :

ScienceClic

Références

Quelques liens relatifs concernant l'effet Terrel.

Les articles originaux

Détail des calculs

Pour aller plus loin


Surprenant, mais pas là où s'y attendait, non ? Ça ne vous donne pas le tournis ?