Jauges

J'ai trouvé un bon samaritain qui a eu le bon goût de donner un exemple assez simple, que j'ai un peu adapté. Il faut dire qu'ils sont très très rares les gens qui vous explique ça sans mathématiques qui vous tuent immédiatement...

L'espace-temps est un écran, une matrice de pixels comme celle que vous êtes en train de regarder (car ça m'étonnerait que vous ayez imprimé cette page web pour la lire).

Chaque pixel est constitué de 3 LEDs, une rouge, une verte, une bleue.

Par convention, on affecte à chaque pixel = à chaque point de l'espace un vecteur composé de 3 nombres, qui représente l'intensité de chaque couleur RGB. Voilà, vous êtes en face de votre premier champ de vecteurs.

La jauge est la manière d'afficher ce vecteur : le premier nombre est l'intensité du rouge, etc.

Nous allons effectuer une transformation de jauge globale sur notre champ de pixels.

Elle consiste à modifier l'ordre des pixels, ce qui va notablement changer les couleurs de l'image, par exemple le rouge devient vert, le vert devient bleu, et le bleu devient rouge. Vous pouvez imaginer des trucs plus compliqués pour le réarrangement des couleurs...

Cette transformation de jauge sera globale car on affecte l'intégralité des pixels de la même manière.

L'image est modifiée, mais encore compréhensible. C'est comme si on avait changé la convention des couleurs.

La différence avec le cas global est simple : à chaque point de l'espace, on affecte une nouvelle convention de couleur, mais pas la même pour tous les pixels. A chaque pixel, on affecte un vecteur de transformation différent, autrement dit on applique un second champ particulier oui, c'est encore un champ de vecteurs, c'est ce qui rend les choses confuses.

Cette fois, ce n'est pas la même histoire, l'image devient incompréhensible.

Pour la décoder, il faudra appliquer un troisième champ de vecteurs (inverse) pour retrouver l'image originale.

A présent, un exemple plus physique : un champ électrostatique généré par une charge ponctuelle. Si vous voyez de quoi je parle, ça devrait aider, normalement vous avez dû voir ça au lycée.

En chaque point de l'espace, on peut mesurer et donner une valeur du champ électrique qui s'exprime en volt par mètre. Ainsi qu'une direction dans l'espace, ce qui en fait un vecteur avec une direction et une amplitude.

Vous avez un champ de vecteurs qui représente le champ électrique.

Notez que si rien ne bouge dans le temps, on parle de champ électrostatique. Eh oui, nous avons aussi la variable temps qui traine toujours avec l'espace... Laissons le temps de côté, c'est déjà assez compliqué.

Si un électron se promène dans le coin, le champ électrique lui appliquera une force, il accélèrera dans la direction du vecteur.

On peut également définir le potentiel électrique. Il s'agit de la tension, exprimée en volt, en chaque point de l'espace. Cette fois, il s'agit simplement d'un nombre. Mais c'est aussi un champ (de scalaires), on a une valeur en tout point de l'espace.

Les électriciens et autres électroniciens voient déjà un problème qui se profile : mais où est la masse ?

En effet, on sait bien qu'on ne peut pas mesurer une tension avec un seul fil, il en faut toujours deux car on parle TOUJOURS de différence de potentiel. Et là, on peut avoir des valeurs différentes suivant la masse que l'on utilise.

Si vous voulez obtenir une mesure utilisable, ce sera mieux d'utiliser la même référence de masse pour toutes les mesures, globalement... Vous devriez commencer à voir se profiler les histoires de "global / local".

En électromagnétisme, il existe un lien étroit entre le champ électrique et le potentiel électrique, et heureusement. Ce sont les fameuses équations de Maxwell qui exprime ce lien.

On peut déduire le champ électrique depuis le champ de potentiel, avec un calcul simple puisqu'il s'agit de faire une soustraction entre deux points de l'espace pour obtenir l'amplitude, la direction étant donnée par les deux points de l'espace. Mais vous le saviez déjà : le champ électrique est en volt par mètre, alors que la tension est en volt.

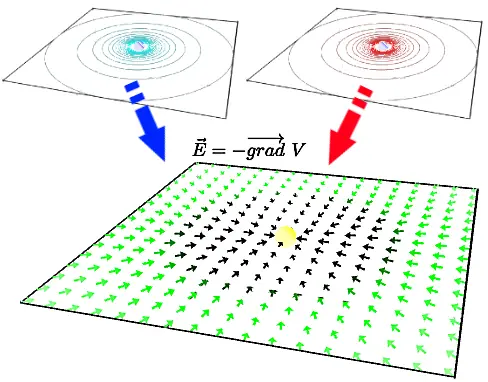
Mathématiquement, il s'agit d'une dérivée par rapport aux coordonnées spatiales. Dans ce cas, on parle de gradient, et on a la relation :

Ce n'est pas n'importe quel champ de vecteurs qui peut être un vrai champ électrique réel. Il faut ajouter des conditions supplémentaires, en particulier il faudra que le rotationnel du champ électrique soit nul.

L'opération inverse aller du champ électrique au potentiel est également possible ─forcément. Dans ce cas, ce sera une intégrale mathématique, et lors de l'intégration, il faudra introduire une constante, inconnue. Habituellement, on la met à zéro, c'est la fameuse masse.

Attention, c'est là que ces histoires de jauges et de symétries deviennent importantes. Mais c'est visiblement compliqué à expliquer, je ne sais pas si j'y arriverai. En attendant, c'est comme ça que le modèle standard des particules est né.

Commençons par prendre une théorie avec des particules libres, sans interactions. Par exemple, notre univers où les chocs n'existeraient pas. Pensez à l'océan de photons qui remplissent la pièce où vous êtes, et chaque photon ignore superbement les autres.

Cette théorie vérifie une invariance de jauge globale donc possède une certaine symétrie. Mais il ne se passe rien, il n'y a pas d'interaction. Chaque particule possède pourtant une énergie, une quantité de mouvement.

On va modifier cette théorie en appliquant une transformation de jauge locale. Ce n'est pas bon du tout, car notre théorie vérifie une invariance de jauge globale ! Ça ne marche pas, la symétrie initiale est détruite.

Prenons un exemple :

• Avant, sans la transformation de jauge locale, la distance entre deux points est constante, on peut comparer les valeurs.
• Avec la transformation de jauge locale, les points ne sont plus à la même place !

Cela met la zone dans la symétrie de translation qu'on avait. La quantité de mouvement, l'énergie, plus rien ne marche correctement !

Pour corriger le tir, on applique alors ce qu'on l'on appelle un champ de jauge, qui va compenser les erreurs introduites par notre transformation de jauge locale :

Les modifications de notre champ de jauge sont également locales. Nous retrouvons les bonnes valeurs entre nos deux points distants, si on s'est correctement débrouillé avec les formules mathématiques.

Le truc étonnant, c'est que ce nouveau champ de jauge est capable de stocker de l'énergie, de la quantité de mouvement, et forcément puisqu'il faut compenser notre transformation de jauge locale. Nous sommes alors en face d'une nouvelle théorie !

Mais la magie intervient au niveau des particules. Initialement, elles s'ignoraient royalement. Dans notre nouvelle théorie, leur comportement est modifié, et on va pouvoir interpréter cela comme une interaction. C'est ce qu'on voulait en appliquant notre transformation de jauge locale, après tout.

Sauf que le nouveau champ de jauge que l'on a introduit pour compenser notre transformation permet l'échange de quantité de mouvement, d'énergie : cela correspond aux particules médiatrices de force, d'échanges.
C'est magique.

D'où le terme "bosons de jauge".

Et pas moins que ça.

En physique théorique, une théorie de jauge est une théorie des champs basée sur un groupe de symétrie locale, appelé groupe de jauge, définissant une « invariance de jauge ». Le prototype le plus simple de théorie de jauge est l'électrodynamique classique de Maxwell.

C'est là que les mathématiques interviennent lourdement, du genre "espace fibré différentiel" avec les "groupes de Lie" rien à voir avec le vin qui comportent certaines symétries. Et en plus, il faut introduire les contraintes de quantification, ce qui ne simplifie pas les choses, afin de coller finalement à ce qui est observé dans les expériences.

En court-circuitant toute explication que je serai bien incapable de détailler :

• dans le cas de l'électromagnétisme, un seul champ de jauge est utilisé, utilisant à U(1) c'est son nom, qui correspond au photon, vecteur de médiation des interactions électromagnétiques
• pour l'interaction faible, ce sont 3 champs, correspondant à SU(2), et aux 3 bosons Z,W+,W-
• électromagnétisme et interaction faible ont été unifiés en l'interaction électrofaible, U(1)×SU(2)
• l'interaction forte, celle qui relie les quarks, requiert 8 champs et 8 gluons associés, correspondant au groupe SU(3). C'est la chromodynamique quantique avec les histoires de couleurs.

Et le Grâal serait de trouver un truc analogue pour la gravitation, afin d'unifier tout ça.

J'espère que ces histoires de jauge sont à présent un poil plus clair.

C'est là qu'on regrette de ne pas avoir bien suivi les cours de mathématiques, vu l'importance qu'elles ont en "simplifiant" et éclairant la physique. Ceci dit, ce sont les physiciens qui ont recours aux maths, et pas l'inverse.

On voit bien que les interactions entre particules sont invariantes sous certaines transformations abstraites qu’on appelle transformations de jauge.

En chaque point d’espace-temps, agit une copie distincte du groupe de transformations. On appelle cela une symétrie de jauge.

Il existe des symétries à tous les étages, qu'il faut convenablement appliquer pour que le modèle s'ajuste correctement à la réalité.

L'invariance de jauge est devenu un des principes fondamentaux de la physique, comme l'invariance de Lorentz ou la localité.