Symétries et lois de conservation
L'observation de symétries a permis d'exhiber certaines propriétés physiques. Et les mathématiques permettent de faire le lien.
Quelques définitions
- Une quantité conservée est une quantité non modifiée. Par exemple, dans un système fermé, sans échanges avec l'extérieur, la quantité d'énergie est toujours la même.
- Une symétrie est une transformation qui laisse invariante les lois de la physique. En d'autres termes, si l’état d’un système est décrit par un ensemble de paramètres (p1, p2 … pn) la transformée (T(p1), T(p2) … T(pn)) doit être également solution des équations du système.
- Une grandeur non-observable est une grandeur dont on ne peut mesurer qu'une valeur relative, dont la valeur absolue n'est qu'une convention. Par exemple, une mesure de tension électrique se fait toujours par rapport à une masse conventionnelle, car on mesure toujours que des différences de potentiel. Non-observable est un mauvais terme, un pis-aller.
Théorème de Noether
La mathématicienne Emmy Noether démontra en 1915 le théorème de Noether, l'équivalence entre les lois de conservation et l'invariance du lagrangien d'un système par certaines transformations.

Tout système qui possède une symétrie possède aussi une grandeur qui est conservée.
Le théorème de Noether démontre l'équivalence entre la conservation d’une grandeur en physique classique et l’existence d’une classe de transformations (=symétrie) qui laisse invariante les lois physiques d’un système.
Lois de conservation
Attention aux absolus
Dans ma page concernant un repère spatio-temporel absolu, on pourrait croire qu'il existe un temps et un espace absolu avec une position privilégiée et une horloge particulière possédant un zéro. Ce n'est pas le cas, je dis simplement que loin de tout comprenez loin de l'énergie, eh bien c'est là que le temps s'écoule le plus lentement et que les longueurs sont les plus longues, ce qui permet de créer une sorte de GPS galactique, avec une référence arbitraire ─évidemment.
Comme on va parler lois de conservation, forcément on va parler de choses impossibles à référencer absolument, ce qui entraine des symétries, et les liens entre les deux.
Energie & temps
Si j'ai pris la rotation comme exemple ci-dessus pour parler du lien entre symétrie et lois de conservation, ce qui m'a le plus marqué est l'équivalence entre l'énergie et le temps, allez savoir pourquoi. C'est évident sans l'être.
Il n'existe pas de temps absolu mais on peut convenir d'un temps zéro pour nous faciliter la vie, tout est relatif, et nos lois physiques sont une expression de cette invariance temporelle.
L'invariance par translation dans le temps entraîne la conservation de l'énergie.
Une bombe, tant qu'elle n'explose pas, autrement dit qu'elle ne change pas dans le temps, conserve son énergie.

Quantité de mouvement
Ce qui s'applique à la dimension temporelle est également vraie pour les dimensions spatiales.
On sait bien que les lois de la physique sont applicables dans tout l'univers, c'est une symétrie fondamentale.
On va distinguer les translations et les rotations.
En ce qui concerne les translations spatiales, l'absence d'un repère spatial absolu ce qui n'empêche pas de convenir d'un repère pour nous faciliter la vie, le GPS par exemple, entraine la conservation de la quantité de mouvement ou impulsion, autrement dit la masse/énergie multipliée par sa vitesse.
L'invariance par translation dans l'espace selon une direction donnée entraîne la conservation de la quantité de mouvement dans la même direction.
C'est certainement la loi qui va nous coûter le plus cher pour explorer l'univers, car envoyer une masse (ou plutôt une impulsion) vers une autre galaxie implique d'envoyer la même à l'opposé.
Moment angulaire
Tout ce qui arrive aux translations s'applique aussi aux rotations. On parle alors du moment cinétique de rotation, ou moment angulaire. C'est l'exemple du spinner que j'ai pris ci-dessus pour introduire le sujet.
Il n'existe pas de direction privilégiée dans l'univers, tout est pareil quelle que soit la rotation que l'on effectue. Pareil que pour l'impulsion.
L'invariance par rotation dans l'espace entraîne la conservation du moment angulaire.
Le plus étrange pour moi est qu'à l'échelle de l'univers, la rotation globale est certainement nulle (au pire constant, c'était comment lors du Big Bang ?). Et pourtant toutes les galaxies tournent. Et toutes les planètes et étoiles tournent aussi. Sans parler des particules où c'est plus problématique à exprimer. A chaque fois qu'un corps se met en rotation, alors on doit "le payer" en effectuant une rotation opposée pour obtenir un moment cinétique nul
Relativité
En relativité restreinte, c'est la transformation de Lorentz qui est symétrique. Cela se traduit par la conservation du vecteur énergie-impulsion.
En relativité générale, ce sont les difféomorphismes ne me demandez pas ce que c'est qui se traduisent par des invariants topologiques .
Potentiel électrique
En électricité, en électronique, on décide d'une masse, d'un potentiel de référence. Il n'existe pas de potentiel absolu, et si on change de référence, on redéfinit le potentiel électrique (on fait ce qu'on appelle une transformation de jauge). Cela se traduit par la conservation de la charge électrique.
On trouve la même chose sous l'appellation "phase de la matière chargée". La mécanique quantique est bizarre, mais on le savait.
Particules indifférentiables
Prenez un paquet de particules. Elles sont toutes identiques, vous ne pouvez pas faire la différence entre deux particules. Mais vous pouvez compter toutes les permutations possibles. A basse énergie, dans leur état quantique fondamental, ces particules présentent un comportement collectif, c'est le condensat de Böse-Einstein.
Renversement de l'espace : P pour Parité
Il n'existe pas de droite ou gauche absolue comme je dis parfois à Madame : "non, l'autre gauche". Ceci dit, on pourrait s'attendre à avoir une symétrie dans un miroir qui ne change rien. C'est la symétrie par renversement de l'espace.
Il s'agit de deux transformations successives, une réflexion dans un plan suivie d'une rotation de 180° par rapport à un axe perpendiculaire au plan.
- La parité renverse les "vrais" vecteurs (impulsion, champ électrique).
- La parité conserve les pseudovecteurs (champ magnétique, moment angulaire, spin).
En particulier, l'électromagnétisme est respecté dans un miroir.
Les particules possèdent une parité intrinsèque :
- paire (+1) pseudovecteur
- ou impaire (-1) vecteur
Les fermions ont une parité opposé aux anti-fermions.
Par convention, on attribue une parité paire aux quarks (et donc impaire aux anti-quarks).
La parité d'un groupe de particules suit une règle particulière (multiplication des parités individuelle et multiplication par -1 à la puissance du moment cinétique orbital).
Renversement des charges : C pour Charge
Il n'existe pas de charge positive ou négative absolue. Un électron est négatif, mais c'est une pure convention, et valable pour la matière ordinaire. Si on conjugue les charges, l'électron devient un anti-électron, un positron positif.
Du coup il existe une symétrie par renversement des charges. Vous échangez la polarité de toutes les charges, autrement dit vous utilisez de l'anti-matière à la place de la matière, et vous devriez obtenir le même résultat.
Violations C & CP
D'une manière inattendue, on a constaté (en 1956, expérience de Mme Wu) que l'interaction faible ne conserve pas la parité, ni la conjugaison de charge ! On pourrait en conclure qu'il existe une droite absolue.
Eh bien non, dans ce cas, il n'y a pas de violation CP, autrement dit si on utilise de la matière ordinaire, on peut définir la droite, mais elle sera inversée si on utilise de l'anti-matière.
Autrement dit, l'anti-matière se comporte comme la matière dans un miroir.
Mais on a aussi trouvé des violations CP ! Ce qui a conduit à la recherche d'une troisième famille de quarks, beauty et top. Et c'est toujours un sujet de recherche actuellement.
Renversement du temps : T pour Temps
Lorsque l'on regarde un film d'un paquet de particule, comment sait-on si on passe le film à l'endroit ou à l'envers ? Eh bien on ne sait pas.
Il existe une symétrie par renversement du temps, mais c'est plus spécieux car on sait bien que la thermodynamique, et surtout son sbire l'entropie, a mis les pieds dans le plat.
On a observé une violation de T dans le domaine des kaons neutres (CPLear 1998) ainsi que pour les mesons (SLAC 2012). Mais sans rapport avec la flèche du temps.
- L'interaction forte et électromagnétique conserve C,P et T
- L'interaction faible brise
- maximalement C et P
- marginalement CP et T
- La symétrie CPT est toujours conservée.
L'asymétrie CP est une condition nécessaire pour expliquer la disparition (apparente) de l'anti-matière dans l'univers. Mais pas suffisante...
Charge de couleur
En physique des particules, la charge de couleur (rouge, vert, bleu) est une propriété des quarks et des gluons, reliée à l'interaction forte, dans le contexte de la chromodynamique quantique. La somme des trois couleurs donnera du blanc=neutre.
La charge de couleur est conservée lors d'une transformation.
Isospin faible
L'isospin faible est un nombre quantique à la base de l'interaction électrofaible.
En interaction faible, les leptons (chargés) se désintègrent toujours en neutrinos et vice versa.
Résumé
La même chose dans un tableau.
| invariance | non observable | symétrie par | loi de conservation |
|---|---|---|---|
| les lois sont les mêmes tout le temps | temps absolu | translation dans le temps | Energie |
| les lois sont les mêmes partout (espace homogène) | position spatiale absolue | translation dans l'espace | Impulsion |
| les lois sont les mêmes dans toutes les directions (espace isotrope) | direction spatiale absolue | rotation dans l'espace | Moment angulaire (cinétique) |
| idem [relativité restreinte] | idem | Transformations de Lorentz + translations espace et temps | Intervalle d'espace-temps, impulsion, moment cinétique, énergie |
| [relativité générale] | + accélération absolue | Difféomorphismes | Invariants topologiques |
| résultats identiques si on augmente la tension partout | potentiel absolu (phase absolue d'un champ de matière chargé) | translation du potentiel électrique | charge électrique |
| pas de différence entre particules | pas d'identité propre des particules | permutation de particules identiques | statistique de Fermi-Dirac Bose-Einstein |
| résultats identiques dans un miroir | droite/gauche absolue | renversement de vecteur/pseudovecteur | parité |
| résultats identiques matière/anti-matière | charge positive/négative absolue | conjugaison de charge | charge |
| pas de différence entre mélanges cohérents différents de quarks colorés | changement de couleur | générateurs de couleur | |
| pas de différence entre mélanges cohérents différents de leptons chargés et de neutrinos | changement d'un lepton en son neutrino | générateurs d'isospin faible | |
Supersymétrie
Les symétries déjà bien connues sont visibles dans le modèle standard de particules :
La supersymétrie est un prolongement du Modèle standard en physique des particules qui prédit une particule partenaire pour chacune des particules du Modèle standard.
On aurait en plus une invariance par permutation d’un fermion par un boson et vice-versa.
Tentant mais spéculatif pour l'instant.
Transformation de portée locale et conservation de la symétrie
Ces histoires de symétrie sont plus subtiles qu'il n'y parait.
Par exemple, en mécanique classique, la quantité de mouvement globale avant et après le choc de deux boules de billard est conservée, c'est la symétrie par translation.
Mais au moment du choc élastique, la quantité de mouvement de chaque bille n'est pas conservée !
On a une espèce de phénomène qui, lorsque d'autres équations physiques sont mises en jeu, s'arrange pour que cette invariance soit reportée à un niveau supérieur, enfin c'est la constatation qu'on peut faire.
Et on peut vraiment se demander comment ça marche. Comment l'univers s'arrange pour que chaque interaction élémentaire sache quoi faire pour respecter la symétrie observée globalement ?
Brisure spontanée de symétrie
On observe des cas de brisure spontanée de symétrie qui ne se reflètent pas dans les équations. Genre flambage d'une structure symétrique comme une barre. Ou une transition para-ferromagnétique. Ou une balle qui descend d'une colline symétrique. En fait, il en existe toute une tirée.
L'exemple de la balle en équilibre en haut d'une colline symétrique est parlant : la moindre modification infinitésimale provoque la brisure de symétrie, et la balle va tomber sur un côté.
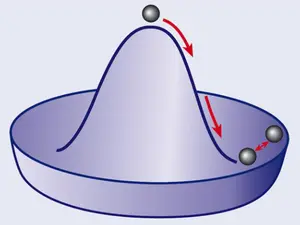
Cette fois, le phénomène précédent où la symétrie est conservée ne se produit pas...
On a défini un paramètre dit paramètre d'ordre qui mesure l'importance de la brisure de symétrie.
Le champ de Higgs (et son fameux boson) a été introduit pour briser la symétrie de l'interaction électro-faible, car les bosons de l'interaction faible ont une masse, alors que le photon pour l'interaction électromagnétique n'en a pas.
En interagissant avec le champ de Higgs, les particules acquièrent une masse.
Voilà, ça faisait un moment que je voulais faire une page sur cette remarque fondamentale concernant l'univers. Vous devriez jeter un œil aux théories de jauge, qui font un usage intensif des symétries.