Améliorer la réception DCF77 avec une plus grande ferrite
Si votre réception du signal DCF77 est mauvaise, c'est peut-être parce que votre ferrite est toute petite. Comment en réaliser une plus grande ?
J'ai été tenté d'améliorer la réception du signal DCF77 en utilisant une ferrite, autrement dit l'antenne, plus grande. Ça n'est pas si évident, et on trouve difficilement de l'information sur le web car la réception des ondes longues avec une ferrite est une technique qui est tombée en désuétude.
L'information que vous trouverez ici est également utile pour tous les récepteurs radio-fréquence de ce type, pas uniquement pour recevoir du DCF77.
Réception
On a vu que pour recevoir le signal radio DCF77, on utilisait une ferrite possédant un bobinage, accordée sur 77.5 kHz.
Plusieurs tailles existent, les plus grosses collectant plus de signal.
Pourquoi ne pas directement acheter un module de réception avec une grande ferrite ? Tout simplement parce qu'on n'en trouve pas.
Il ne s'agit pas simplement de récupérer le bobinage et de le placer sur la nouvelle ferrite. Ce serait trop simple !
Fréquence de résonance
La première chose à saisir, c'est qu'il s'agit d'un couple entre une bobine présentant une induction L avec une capacité C. Le circuit LC formé va résonner à sa fréquence propre donnée par la formule de Thomson.
Il faudra, à un moment ou à un autre, vérifier cette fréquence de résonance, et ça peut se faire assez simplement avec un générateur de fréquence (aux alentours de 77.5 kHz pour notre affaire, c'est très facile à générer), et un oscilloscope pour voir le signal. La méthode est d'ailleurs indiquée dans les datasheets des circuits intégrés de détection.
La sortie du générateur passe dans un fil qui fait plusieurs tours autour de la ferrite, ce qui induit un champ magnétique, qui génère, par l'intermédiaire de la bobine de réception, un courant qui est lu par l'oscilloscope.
On conseille d'utiliser la division par 10 de la sonde pour réduire la capacité parasite ajoutée par la sonde, qui généralement se situe dans la dizaine de picofarads. Mais ce n'est pas vraiment un gros problème dans notre cas, car les valeurs typiques sont :
- quelques millihenrys pour l'inductance
- de l'ordre du nanofarad pour la capacité
Vous pouvez essayer directement sur votre module de réception, ça marche très bien, c'est même impressionnant de voir que le signal enfle énormément lorsqu'on s'approche de la fréquence de résonance. Vous allez mettre l'amplification de l'oscilloscope au maximum au début (sensibilité dans la dizaine de mV), puis vous allez réduire cette amplification en approchant (vous obtiendrez des volts).
Facteur de qualité Q
L'augmentation de la tension traduit le coefficient de surtension Q ou facteur de qualité. En gros, ce coefficient vous donne l'efficacité de votre circuit, plus il est élevé et plus vous aurez de signal à la fin.
Notez que vous n'aurez pas plus de puissance avec un fort Q. Vous aurez seulement plus de tension, le courant diminuera. Mais avec plus de tension, ce sera plus facile d'extraire le signal désiré.
Comme on peut le voir, plus le coefficient Q est élevé, et plus étroit est le pic, autrement dit la bande passante se réduit, ce qui est bon pour sélectionner uniquement le signal de la fréquence désirée.
À la fin, le facteur de qualité dépend de pas mal de paramètres, en particulier les résistances parasites, comment est fait le bobinage, le matériau le matériau de la ferrite, les fils de connexions... Pour avoir un bon Q, il est préférable d'utiliser de gros fils de cuivre pour la bobine afin de réduire la résistance.
D'un autre côté, un Q élevé signifie une bande passante plus étroite, et les variations de température peuvent faire varier l'inductance de la bobine, et on pourrait se retrouver en dehors de la fréquence cible...
Un point à retenir : il existera toujours une résistance dans le circuit, on est plutôt en face d'un circuit RLC. Mais cette résistance est généralement négligeable pour ce qui nous intéresse. Ceci dit, si jamais votre facteur de surtension Q est trop élevé, vous pouvez toujours l'amoindrir en ajoutant une résistance, ce qui ne changera pas la fréquence de résonance. Mais augmentera la bande passante.
Objectif
J'ai commandé plusieurs modules différents, mais à chaque fois je me suis retrouvé au mieux avec une ferrite de 60 mm de long pour un diamètre de 10 mm dans le meilleur des cas, quand ce n'était pas une ferrite plate, donc encore moins efficace, ou carrément pas de ferrite du tout, mais il faut s'attendre à tout quand on commande chez les Chinois pour un prix dérisoire.
J'ai vérifié avec la méthode ci-dessus que la fréquence de résonance était correcte, ce qui m'a permis de me faire la main, et au moins j'aurai une méthode pour la mise au point.
J'ai également commandé des ferrites de 200 mm de long, avec le même diamètre que celles de 60 mm. L'idée est de remplacer une petite ferrite par une plus longue, et le plus simple est de ne pas modifier les modules de réception, ce qui implique de garder la même capacité si possible.
Notez que si vous mettez dans le prolongement d'une ferrite une autre ferrite, alors grosso-modo vous allez vous retrouver comme si vous aviez une ferrite plus longue, et donc vous modifiez (augmentez) l'inductance et la fréquence de résonance (il faudra réduire la capacité, le produit LC doit rester constant).
Capacité et inductance
La capacité et l'inductance sont les deux paramètres qui définissent la fréquence de résonance. J'ai donc analysé ce que j'avais reçu.
- Les capacités déjà présentes valent environ 1.9 nF (ce qui rend les 10 pF de la sonde d'oscilloscope négligeable).
- Ceci implique que l'inductance de la bobine vaut 2.2 mH (via la formule de Thomson pour 77.5 kHz).
Les capacités ne posent pas de problème particulier, on peut même trouver des capacités ajustables, qui ne sont jamais utilisées dans ces modules pour des questions de coût et d'encombrement. Et on peut ajuster finement en déplaçant la bobine sur la ferrite, car l'inductance dépend de ce placement, c'est pour ça que l'on retrouve de la cire sur les bobines.
C'est essentiellement l'inductance qui est à concevoir. Les paramètres critiques dont dépend l'inductance sont les suivants :
- Perméabilité magnétique relative de la ferrite.
- Longueur et diamètre de la ferrite.
- Diamètre de la bobine qui sera réalisée (proche du diamètre de la ferrite, évidemment).
- Section du fil de cuivre utilisé.
- Décalage de la bobine par rapport au centre de la ferrite.
- Nombre de couches d'enroulement, épaisseur entre chaque couche...
Et c'est juste le cas d'une ferrite cylindrique.
Perméabilité magnétique relative
Commençons par examiner le paramètre de base, la perméabilité magnétique relative de la ferrite, car on se doute bien que les propriétés magnétiques sont cruciales pour l'inductance, elle en dépend directement.
Les fabricants de ferrite mettent en avant les propriétés des matériaux qu'ils conçoivent, et il est difficile de choisir car il n'existe pas de matériau ayant toutes les qualités à la fois. On trouvera une liste instructive sur le site de TDK, où on trouve toutes les ferrites proposées, et on constate que la perméabilité varie entre 80 et 10 000 !
L'expérience dans le domaine des grandes ondes montre qu'il faut utiliser des ferrites en Manganèse-Zinc. Dans la liste TDK, il s'agit des ferrites "Filter coil", et quand on regarde les fiches techniques, c'est bien du MnZn. Par exemple les N48, M33 et M34. Et là, c'est le drame. Ça dépend de la fréquence et de la température...
Remarquez l'existence d'une température dite de Curie où le matériau perd irrémédiablement ses propriétés, mais ce sera sans conséquence pour nous.
Si la fréquence de 77.5 kHz ne semble pas poser de problème particulier (la perméabilité est stable dans cette zone pour n'importe quel type de ferrite MnZn), la variation en température n'est pas vraiment négligeable, Pour l'exemple ci-dessus, on voit une variation de l'ordre de 0.15% par degré, autrement dit notre fréquence de résonance va varier dans les mêmes proportions. Pour 77.5 kHz à 20ºC, on aura 78.6 kHz à 30ºC, vaudrait mieux que la bande passante soit assez large.
Or la bande passante, le facteur de qualité et la fréquence de résonance sont liés par la relation QBw = f, alors avec un Q de 300, on aura une bande passante de 77.5/300=0.25 kHz. Oups ! Il ne faudra pas s'étonner de difficulté de réception si le Q est trop fort avec un changement de température.
Les vendeurs chinois ne fournissent pas d'informations techniques précises sur les ferrites vendues, et on peut se douter qu'il s'agit des moins chères. Mais que vaut la perméabilité ? Nous allons tenter de la déduire avec le matériel reçu.
Théorie
Calculer l'inductance d'une bobine sur une ferrite n'est pas évident, même pour le cas particulier de la réception RF. Ce genre de calculs est ancien, du temps où on utilisait les grandes ondes. Par exemple :
- [2004] Ferrite Rod Antennas for HF ?
/ R.H.M. Poole
est un document très intéressant, car il détaille le fonctionnement. Il fournissait même le mode d'emploi pour calculer une antenne avec le fichier Excel mais ce fichier lui-même est introuvable (j'ai pourtant fouillé archive.org).
Voici quelques résultats extraits de ce document.
Position de la bobine
La position de la bobine par rapport au centre de la ferrite est un élément important, car l'inductance va quand même beaucoup varier, comme le montre cet exemple :
Cette propriété permet un ajustement fin de la fréquence de résonance en déplaçant la bobine le long de la ferrite. C'est pour ça qu'on les trouve pratiquement toujours sur les côtés, pas exactement au centre.
Rapport longueur/diamètre
La taille de la ferrite compte, en particulier le ratio longueur par rapport au diamètre :
Actuellement, ce sont souvent des ferrites de 60 mm pour un diamètre de 10 mm, soit un ratio de 6, et je souhaite passer à une ferrite de 200 mm, soit un ratio de 20, ce qui devrait donner nettement plus de signal.
À vue de nez, d'après ces résultats, l'inductance devrait augmenter de 60 %, en conservant le même bobinage. Il faudra donc diminuer le nombre de tours d'autant.
D'autres résultats intéressants :
- Vaut mieux faire une petite bobine par rapport à la taille de la ferrite.
- Le diamètre de la bobine par rapport à celui de la ferrite a très peu d'impact.
Tout ceci laisse l'impression que ce qui complique les choses, c'est que la ferrite "cachée" par la bobine voit sa perméabilité drastiquement modifiée.
Outre le document de Poole exploité ci-dessus, quelques références éventuellement utiles :
- Deux utilisations du ferrite en Radio
/ Robert Berranger, F5NB
Cet article va traiter de l'utilisation du ferrite doux, d'une part pour obtenir des bobines à fort Q utilisées dans le filtrage et d'autre part, pour améliorer la sensibilité des antennes cadres. Pour ces dernières, je décris une suite d'expérimentations avec analyse des résultats qui permettent de mieux cerner les effets des différents paramètres de construction - Une antenne pour les ondes longues 50 à 200 kHz
- [2013] Design of a ferrite rod antenna for harvesting energy from medium wave broadcast signals a le bon goût de présenter comment se calcule la perméabilité.
- WWVB Loopstick Antenna & C-Max Receiver : Brooke Clarke a vraiment fait pas mal d'expérimentation, j'ai découvert son site tardivement. Beaucoup de références également.
Examen de modules
J'ai reçu 5 modules que j'ai examinés.
Module MASD-S-R1
Là, c'est facile, j'ai reçu le module sans ferrite.
La capacité vaut 1.86 nF. La valeur standard est 1.9 nF, avec une précision de 10% (on peut faire confiance aux chinois pour choisir le moins cher).
Pour la fréquence de résonance de 77.5 kHz, il faudra une inductance d'environ 2.2 mH.
Module RCC02 C03A
Probablement du 29 AWG (environ).
La capacité C1 vaut 2.05 nF. L'inductance doit donc valoir 2.06 mH.
Module RC8000
Ils ont tous utilisé du 31 AWG (environ). Les capacités valent :
- RC8000 16 mm : 3.70 nF d'où 1.14 mH.
- RC8000 15 mm : 3.80 nF d'où 1.11 mH.
- RC8000 petite ferrite : 3.81 nF d'où 1.10 mH.
Sans surprise, il s'agit de la même capacité pour tous les modules, à la tolérance près. 3.9 nF est la valeur normalisée, à 10 % près.
Ce qui est plus surprenant, c'est que la bobine du RCC02 avec 121 tours et une ferrite qui semble du même tonneau fait le double d'inductance. Une telle différence est étonnante, et la seule explication est forcément dans la perméabilité initiale de la ferrite.
Performances
J'ai testé en parallèle les 4 modules fonctionnels, et voici le classement basé sur la tête des signaux reçus à l'oscilloscope.
- RC8000 bobine "16 mm"
- RCC02
- RC8000 bobine "14 mm"
- RC8000 petite ferrite
Sans surprise, la plus petite ferrite collecte le plus de bruit. Les deux RC8000 à ferrite 60 mm paraissent quasiment identique, mais il est possible que la bobine soit mieux réalisée et mieux accordée. Le RCC02 est très proche du premier, mais j'ai observé un poil de bruit en plus.
Je trouve quand même étonnant que toutes les photos et tous les modules que j'ai pu voir aient systématiquement la bobine à la même place. Je les soupçonne de faire simple, sans vraiment passer de temps à accorder finement le système...
J'ai l'impression que la bande passante est suffisamment large pour que ça marche raisonnablement.
Passer à une ferrite de 200 mm
Il se trouve que C-MAX a publié une page pour guider dans la réalisation d'une antenne pour le U4223, et qu'ils disent de suivre la même démarche pour le CME6005. Et c'est le DCF77 et ses 77.5 kHz qui est pris en exemple !
Je ne vais donc pas faire mon malin et suivre l'exemple pas à pas, puisque le CME6005 équipe le RCC02. Je suis plus ou moins le chapitre 2 "Practical antenna design".
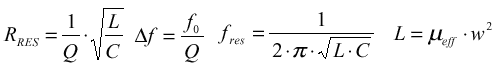
| U4223 | CME6005 60 mm | CME6005 200 mm |
|
|---|---|---|---|
| fréquence | 77.5 kHz | ||
| choix R res | 180 kΩ | 100 kΩ (40 à 100 OK) | |
| choix Q | 100 | 100 (réduire si pb de température) | |
| Bande passante | 0.775 kHz | 0.775 kHz | |
| Capacité C | 1.14 nF | 2.05 nF (mesure) | |
| Inductance L | 3.5 mH | 2.05 mH | |
| Connexion | single ended (1d) | ||
| Perméabilité initiale | 2000 (estimée) | ||
| Perméabilité effective | mesurer l'inductance avec 100 tours | ||
| Diamètre fil | 0.28 mm (pas moins de 0.15, 0.3 mesuré) | ||
| ajuster à la fin en déplaçant la bobine | |||
| Nombre de tours | 121 | ||
| Perméabilité effective | 140.10⁻ ⁹ | ? | |
Je suis "remonté" à la perméabilité effective grâce au module RCC02 qui est fonctionnel. Et là, je reste le bec dans l'eau quand il s'agit de calculer la bobine puisque je ne connais pas la perméabilité effective pour ma ferrite de 200 mm. Il nous faut une formule de calcul plus adaptée, à partir de la perméabilité initiale.
Ça vaudra ce que ça vaudra, je commencerai par supposer que la perméabilité de ma ferrite de 200 mm est la même. Mais bon, sur les 4 exemples que j'ai reçus, la RCC02 présente manifestement une valeur inférieure.
Calcul de bobine
Trouver un calculateur, ou au moins une formule pratique est une sinécure.
Voici quelques résultats décevants :
- Single-layer Coil Inductance and Q mais pas pour les ferrites
- Ferrite Rod Coil formule inadaptée pour notre cas, aucun calculateur
- Rod Permeability Calculator / Fair-Rite évalue la perméabilité, pas utile
- Inductance of Solenoids on Ferrite Rods donne des résultats empiriques pratiques
- Advanced Inductor Calculator de SimpliTools ne vaut pas un radis.
J'ai cependant trouvé le calculateur de Coil32 : Coil on a ferrite rod et Ferrite rod core inductance la page justifiant les formules.
Il présente le défaut de ne pas tenir compte d'enroulements superposés, mais comme je n'ai rien trouvé d'autre, je vais faire avec. Après tout, je n'ai besoin que d'un résultat approché, je passerai forcément par une expérimentation pratique et un ajustement, que ce soit en retirant ou en ajoutant un tour de plus ou en déplaçant la bobine.
Pour commencer, j'essaye d'obtenir mes 121 tours sur le cas des 2.05 mH sur une ferrite de 10x60 mm. Mais dans ce cas précis, les formules ne sont pas adaptées, impossible d'approcher le résultat.
J'essaye alors avec 1.1 mH et 144 tours, en faisant attention d'avoir une longueur de bobinage de 16 mm, car c'est essentiellement lui qui "cache" la ferrite, il faut laisser à la ferrite une taille "externe" efficace plausible. Cela m'oblige à utiliser du fil plus mince (38 AWG), mais ce n'est pas critique. Du coup j'obtiens une perméabilité relative de 30, ce qui parait faible, mais bon, l'important est d'utiliser la même à présent.
Tous les autres paramètres identiques, je passe à 200 mm, et j'obtiens : 119 tours (au lieu de 144). Cela parait plausible. En déplaçant la bobine sur un bout, à 70 mm, l'inductance se réduit et il me faut à présent...145 tours !
Autrement dit, il suffirait de démonter la bobine d'une ferrite de 60 mm, et de la mettre directement sur la ferrite de 200 mm, puis d'ajuster sa position. Incroyable.
Réalisation
Je fabrique donc une bobine similaire à celle déjà existante, avec 130 tours pour démarrer, que j'ai réduit à 120 tours après un premier essai. L'ajustement de la fréquence de résonance fut assez facile, bien qu'imprécise avec mon matériel. Et la comparaison avec le meilleur résultat des tests précédents fut sans appel :
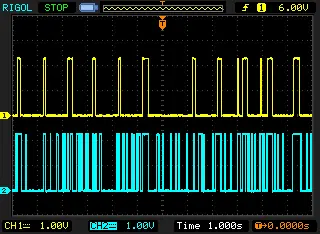
le "trou", c'est le début de minute
yapa photo
J'ai tenté d'en savoir un peu plus sur le facteur de qualité, mais je n'ai pu que mesurer avec difficulté le passage de 800 à 850 mV maximum (avec mon montage) à 100 mV entre 74.6 et 81.3 kHz, soit 6.7 kHz pour un facteur 8. La bande passante à -3 dB (565 mV) était théoriquement de 0.77 kHz, ce qui me donne l'impression d'un facteur de qualité pas extraordinaire, du coup je ne serai pas gêné par la température.
N'hésitez pas à faire votre propre antenne avec une ferrite de 200 mm. Bobinez 120 tours, puis ajustez avec l'aide d'un générateur de signaux sinusoïdaux, une boucle sur la ferrite et un oscilloscope pour voir le signal maximum pour votre module de réception préféré.
Ah oui, quand même !