DCF 77
Comment se passe la propagation du signal ? Comment choisir un module de réception DCF77 ? Et ça s'achète où ?
Voici le résultat de mes recherches en 2025, en espérant que ça vous aidera un peu. Vous trouverez une liste de puces électroniques à connecter à une antenne en ferrite, mais vous serez plus probablement plus intéressés par les modules de réception de l'heure radio-diffusé.
Commençons par la propagation des signaux.
Propagation
Le 77.5 kHz se propage de diverses manières, en particulier quand on est assez proche de l'émetteur, on reçoit ce qu'on appelle une onde directe ou une onde de sol (du coup avec pas mal de puissance car on est proche). Il faut aussi savoir que les ondes se reflètent plus ou moins dans l'ionosphère, constituée de diverses couches.
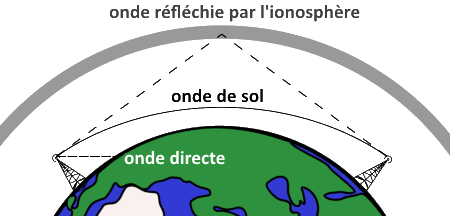
Sauf que les couches ionosphériques sont différentes entre le jour et la nuit, excitées par le soleil, modifiant notablement les réflexions et la propagation des ondes.
Du coup le signal n'est pas toujours le même durant 24h, et sera également perturbé par les multiples réflexions...
Accessoirement, le temps de propagation varie suivant la propagation, directe ou en réflexion, on parle de centaines de microsecondes !
Le bon côté est que l'on reçoit mieux et plus loin les ondes la nuit.
Réception
À ces fréquences-là, on reçoit les signaux radio avec une ferrite possédant un bobinage, accordée sur 77.5 kHz. En effet, la longueur d'onde vaut 3868 m, alors installer une antenne quart d'onde de 967 m n'est pas envisageable pour la plupart des applications.
Plusieurs tailles existent, les plus grosses recevant plus de signal.
Comme la polarisation est horizontale, il faudra orienter la ferrite pour maximiser le signal reçu de la manière suivante :

Une boussole vous évitera de chercher...
Ce qui n'est pas exempt de bruit, car le moindre parasite se traduit par un (petit) créneau dans le signal, ce qui est généralement très gênant pour l'amateur qui est désarçonné par le fait que ce n'est pas parfait, et ne s'y attendait pas, ce qui plombe complètement son joli programme de décodage...
Ces antennes ont tendance à collecter tout le bruit environnant, et notoirement les TV et autres écrans de PC, il faudra éloigner la ferrite autant que possible de toute électronique, en particulier celle qui contiendra votre microcontrôleur dans lequel vous allez mettre le joli code que vous allez faire. Faites des essais...
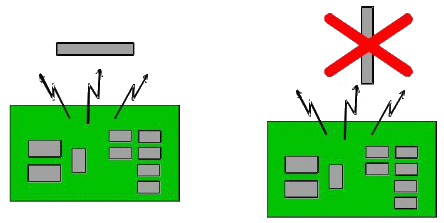
Ne pointez pas la ferrite vers une électronique bruyante...
Plus l'antenne est longue, mieux c'est
Plus l'antenne en ferrite est grande, et plus vous aurez de signal. L'amélioration sera importante, surtout dans les cas de mauvaise réception, comme pour moi dans les Alpes françaises, ou si vous n'avez pas de place pour orienter correctement l'antenne.
Si on a de la place, on est tenté d'augmenter la taille de l'antenne, en remplaçant la petite ferrite par une grosse, par exemple par une de 200 mm. C'est une bonne idée, sauf que :
- L'inductance de la ferrite va changer, et donc il faudra refaire l'accordage à 77.5 kHz
- La valeur de l'inductance dépend de la taille/forme de la ferrite
- La valeur dépend aussi de la position sur la ferrite, ce qui est d'ailleurs un moyen d'accorder finement l'antenne pour les constructeurs.
Mais c'est parfaitement faisable, assez facilement.
Notez qu'il existe forcément une capacité avec l'inductance, l'ensemble étant accordé sur 77.5kHz. Parfois cette capacité est directement collée sur la ferrite, sinon elle est reportée sur le circuit imprimé.
Ceci dit, ma montre-bracelet reçoit très bien le signal la nuit. Et l'antenne est minuscule...
Circuits
Un module de réception est censé collecter le signal, et le transformer en créneaux électriques, bêtement à "zéro" quand la modulation est présente, et montant à "un" lorsque la modulation est descendue à 15% (ou l'inverse, ça ne changera que la lecture par votre horloge, une chance sur 2 que ce soit bon).
Composants discrets
Vous pouvez être tenté de réaliser votre module vous-même, en utilisant des composants simples, on parle alors de circuits discrets. Il faudra être plutôt bon en réception analogique, à l'ancienne. Si vous savez comment marche un vieux récepteur à transistors, grandes ondes et petites ondes, alors vous pouvez éventuellement vous risquer. Il vous faudra aussi le matériel de mesure adéquat.
- Un récepteur utilisant la bonne vieille technique superhétérodyne des radio à transistors d'antan : A DCF77 Superheterodyne Receiver. Si on améliore la réception du signal au plus tôt, et bien ça marchera bien mieux que de tenter de filtrer plus tard...
- An active DCF77 antenna
- DCF77 Preamplifier Car il vaut mieux amplifier le signal au plus tôt.
- [2013]53 Standard de fréquence verrouillé sur DCF77 la réception est faite en éléments discrets (Électronique Pratique numéro 388).
Circuits intégrés
Les entreprises de microélectroniques ont proposé des circuits spécialement conçus pour réaliser la réception, souvent en BiCMOS. Il suffit de connecter à l'entrée une antenne accordée à la fréquence désirée, ainsi qu'adjoindre un quartz à la même fréquence, (77.5 kHz pour le DCF77), puis de binariser en 0 ou 1 suivant l'intensité des signaux.
Ces circuits sont à la base des modules prêts à l'emploi, où il suffit d'ajouter les quelques capacités difficilement intégrables.
Modules prêts à l'emploi
Ces modules sont immédiatement utilisables et présentent une consommation ridicule (moins de 100 μA), pas chers (on parle de quelques euros). Vous aurez du mal à faire mieux.
Récupération
Une solution assez simple pour se procurer un module consiste à dépouiller une horloge DCF77 de son module de réception, car les constructeurs ne se sont pas cassés la tête : c'est tentant de récupérer des modules chinois pas chers. Choisissez une pendule bas coût, et essayez d'obtenir une photo de l'intérieur. Plutôt un modèle électronique, genre radio-réveil radio-piloté, pas mécanique, car c'est souvent le même mécanisme asservi, et le module n'est pas séparé.
Un avantage de cette solution est que vous pourrez observer les tensions et signaux en fonctionnement normal. Sauf qu'il faudra forcer la lecture, car souvent ces pendules ne lisent les signaux qu'une seule fois en 24h, la nuit.
Achat
Mais bon, si vous voulez en acheter un, lequel prendre ? Vous allez vous retrouver comme Udo Klein, à en commander plusieurs pour les tester :
- Blinkenlight / DCF77 Receiver Modules tests par Udo Klein.
J'ai péniblement collecté des informations sur les modules de réception. Leur identification est délicate, surtout les modèles revendus sur des sites chinois. Certains sont probablement obsolètes, plus disponibles, mais bon, on les retrouve parfois sous d'autres noms. Ne les ayant pas testés, je ne sais pas ce qu'ils valent, tenez-le pour dit. Ceci dit, c'est d'abord l'antenne qui fait le boulot, c'est la partie la plus importante. Après, on fait ce qu'on peut avec le niveau de signal à bruit qu'on reçoit.
Faites très attention sur les images des sites chinois : elles sont parfois très fantaisistes, avec des versos ne correspondant pas aux rectos. Ou des images différentes pour un seul produit.
Vous trouverez des modules facilement sur Aliexpress, et les mêmes en bien plus chers sur Amazon, Ebay et consorts. La difficulté est l'énorme quantité de revendeurs, et les descriptions disparates. Finalement, il n'y a pas tant de modules que ça. Mais quasiment tous vous propose une petite antenne.
Les listes suivantes et les informations devraient vous aider à vous mettre sur la voie, ou pire, rendre les choses encore plus confuses, désolé. Mais au moins, vous saurez dans quel guêpier vous allez.
Liste des circuits intégrés de réception
J'ai recherché ces entreprises et les circuits de réception, et il n'y en a pas tant que ça. Ceci dit, je ne suis pas certain d'avoir trouvé tous les circuits, surtout lorsqu'ils sont vendus sous forme de puce nue et non en boitier, car les puces nues ne sont utilisables que par un faible nombre de compagnies équipées du matériel adéquat, et donc les datasheets restent à une diffusion confidentielle.
Cliquez sur la compagnie pour avoir plus de détails.
Rangé par ordre d'apparition sur le marché.
| Compagnie | Datasheet | |
|---|---|---|
| Telefunken Temic Atmel | 2775 / 422x | |
| 1986 | TFK U2775B | |
| 1996 | Temic U4221B | |
| 1996 | Temic U4222B | |
| 2001 | Atmel U4223B | |
| 1996 | Temic U4224B | |
| 1996 | Temic T4225B | |
| 1999 | Temic U4226B | |
| HKW-Elektronik | UE2125 / UE601x | |
| 1994 | HKW UE2125 | |
| 2006 | HKW UE6015 | |
| GSG Günther Semiconductor | AK212x | |
| 2000 | GSG AK2124 | |
| 2000 | GSG AK2125 | |
| 2000 | GSG AK212 TFA2127 |
|
| Sanyo | LA165x | |
| 2000 | Sanyo LA1650 LA1650C | |
| 2006 | Sanyo LA1652C | |
| 2006 | Sanyo LA1654C | |
| 2006 | Sanyo LA1654FN | |
| MAS Micro Analog System | MAS61xx / MAS91xx / MAS101x | |
| 2007 | MAS6179 | |
| 2025 | MAS6180D | |
| 2014 | MAS6181B | |
| 2025 | MAS6181C | |
| 2004 | MAS9078 | |
| 2005 | MAS9079 | |
| 2003 | MAS9178 | |
| 2005 | MAS9179 | |
| 2005 | MAS9180 | |
| 2000 | MAS1016A | |
| 2002 | MAS1017A | |
| OKI | ML6190 | |
| 2003 | OKI ML6190A | |
| 2005 | OKI ML6190B | |
| NPC Nippon Precision Circuits | SM950x | |
| 2004 | NPC SM9501A/B | |
| 2010 | NPC SM9501A | |
| 2007 | NPC SM9501B | |
| 2004 | NPC SM9502A | |
| 2004 | NPC SM9503A | |
| C-MAX | CME6005 / CME8000 | |
| 2007 | C-MAX CME8000 | |
| 2004 | C-MAX CME6005 | |
| 2022 | C-MAX CME6005 2022 | |
| Silicore | D6002 | |
| 2010 | Silicore D6002 |
La même chose, simplifiée, par numéro.
| Telefunken / Temic / Atmel | 2775 422x |
| GSG Günther Semiconductor | AK 212x |
| C-MAX | CME 6005 CME 8000 |
| Silicore | D 6002 |
| Sanyo | LA 165x |
| MAS Micro Analog Systems | MAS 101x MAS 61xx MAS 91xx |
| OKI | ML 6190 |
| NPC Nippon Precision Circuits | SM 950x |
| HKW-Elektronik | UE 2125 UE 601x |
Finalement, assez peu de circuits, et pas de nouvel acteur depuis 2010. Et pourtant, je m'y connais en microélectronique, c'est mon métier de base, je sais comment chercher. Sauf qu'Internet s'est répandu un peu plus tard. Je n'ai trouvé aucun site qui rassemble ce genre de circuits...
Liste des modules de réception
La liste suivante est là pour vous aider à identifier le module bizarre que vous venez de trouver chez Aliexpress ou Amazon. Vous avez déjà eu l'impression de le voir, et vous vous demandez si c'est le même que l'autre qui coûte trois fois moins cher ?
Attention : chapitre spécial à la fin pour tout ce que je n'ai pas pu identifier. En particulier une section QiXin / jfd-ic.com, des Chinois qui déclarent une tirée de modules et d'horloges.
Cliquez sur l'image pour avoir plus de détails.
















Temic 422x
Temic fut une société de semiconducteurs issue de Telefunken (TFK), et qui a été rachetée (par Atmel, où je bossais), la marque a disparu.
Le premier circuit intégré d'horloge radiopilotée fut le U2775B, créé en 1986 par Telefunken, pour la compagnie Junghans. Un circuit intégré compatible avec les montres-bracelets a suivi en 1990.
- [1986] TFK U2775B
- [1996] Temic U4221B datasheet
- [1996] Temic U4222B datasheet
- [2001] Atmel U4223B datasheet
- [1996] Temic U4224B datasheet
- [1996] Temic T4225B datasheet
- [1999] Temic U4226B datasheet
La datasheet du circuit U2775B est introuvable, mais vous trouverez des schémas d'utilisation.
Certaines datasheets détaillent les protocoles des horloges.
Le circuit U4224 exige une antenne avec un facteur Q d'au moins 30. La datasheet vous donne la procédure pour mettre votre antenne au point, en utilisant un générateur 77.5 kHz, et un oscilloscope, puis une calculatrice. Ils vous recommandent même de faire attention si jamais vous observez des grosses variations de température...
Ce circuit requiert normalement 2 quartz à 77.5 kHz, mais l'un des deux peut être remplacé par une capacité de 10 pF.
Conrad / Sélectronic
Ce vieux module DCF n'est apparemment plus disponible chez Conrad. Notez la toute petite antenne. Sélectronic avait manifestement le même.
- [2002] DCF pour le PICÉE / Elektor 292 (schéma page 28)
- Module réception horloge radio-pilotée DCF 77 Pro (Sélectronic) [Archive Club-Elec]
HKW-Elektronik UE601x
HKW est une entreprise allemande qui propose :
- les antennes en ferrite
- les modules de réception
- utilisant leurs propres circuits intégrés
Sauf qu'en 2025, ils n'ont plus de boutique où on peut les acheter.
- [1994] UE2124
- [1994] HKW UE2125 datasheet+
- UE6002
- UE6010
- UE6011
- [2006] HKW UE6015 datasheet préliminaire
Il doit exister toute la série de UE60xx.
Ces modules seraient d'excellente qualité. Comme on peut s'y attendre pour des Allemands. Il en existe toute une tirée, depuis le temps qu'ils en font !
Modules
- [1994] Module EM1 Conrad
- [1998] HKW EM2 module avec le UE6002
- [2002] HKW EM6 module
Conrad EM1
[1994] Un antique module de réception Conrad utilise le UE2124.
GSG Günther Semiconductor AK212x
Günther Semiconductor GmbH est une compagnie fabriquant des wafers silicium, apparue vers 1960 et disparue depuis des lustres, dont on ne retrouve presque aucune trace (gsg-asia.com).
On remarquera l'étrange similitude des diagrammes entre GSG et HKW.
Puces
- [2000] GSG AK2124 datasheet edition 09/00
- [2000] GSG AK2125 datasheet edition 09/00
- [2000] GSG AK2127 TFA2127 datasheet edition 09/00
Pour ne pas arranger les choses, ils utilisent d'autres références dans leur propre datasheet, l'AK2127 s'appelle TFA2127 dès la première ligne, référence qui n'a pas l'air d'exister.
On ne retrouve que les datasheets, pas la moindre trace d'un module employant une de ces puces.
Sanyo LA1650
Sanyo est une marque japonaise bien connue. Sanyo Semiconductors a été intégré à On Semiconductors.
- [2000] Sanyo LA1650 LA1650C datasheet
- [2006] Sanyo LA1652C datasheet
- [2006] Sanyo LA1654C datasheet
- [2014] OnSemi LA1654C datasheet (obsolète)
- [2006] Sanyo LA1654FN datasheet
Ces circuits sont tous obsolètes.
Micro Analog Systems MAS
Micro Analog Systems est une entreprise finlandaise proposant pas mal de références et plutôt active sur le sujet des acquisitions de signaux horaires. On va retrouver des modules réalisés par leurs soins, et leurs puces doivent souvent être utilisées, ils doivent équiper pas mal de solutions sans qu'on le sache...
Comme souvent, MAS propose aussi du « dual band », par exemple 77.5 kHz et 60 kHz (la fréquence anglaise), et on pourra voir deux emplacements de quartz.
Site web
Puces
- [2007] MAS6179 datasheet préliminaire
- [2025] MAS6180D datasheet 5.5 volt
- [2014] MAS6181B datasheet (obsolète, 3.3 volt max)
- [2025] MAS6181C datasheet
- [2003] MAS9078 datasheet
- [2004] MAS9078 datasheet (2004)
- [2005] MAS9079 datasheet
- [2003] MAS9178 datasheet
- [2005] MAS9179 datasheet
- [2005] MAS9180 datasheet
- [2000] MAS1016A datasheet
- [2002] MAS1017A datasheet
Modules
Notez la resistance R1 de 100 Ω en série avec l'alimentation.
Le module DL8173 utilise le MAS6181, et est fabriqué par QiXin / jfd-ic.com. Lequel Chinois propose toute une tirée de modules et d'horloges, ça ne m'étonnerait pas plus que ça qu'ils soient les principaux fournisseurs.
Reichelt
La datasheet (dispo sur le site de Reichelt) date de 2007, dernière version en 2011.
ELV DCF-2
ELV propose aussi un module fait avec les puces de MAS.
- ELV DCF-Empfangsmodul DCF-2 (ELV)
- Real-Time-Clock RTC-DCF mit DCF77-Empfang où le module est inséré sur une carte ad-hoc.
Datasheet dispo sur le site d'ELV.
Canaduino
Un module canadien avec un nom pareil apparemment de bonne qualité, qui utilise le circuit MAS6180C. Ont ajouté une puce pour piloter quelques LEDs, et ont fait « classique », pas de chip-on-board.
MJU-823
On trouve un module sous divers noms, par exemple JJY-1060N-MJU, Occus, qui est aussi basé sur la puce MAS6181. Faites attention à la bande utilisée, si c'est 40-60 kHz, c'est pour le Japon !
D002AA
OKI ML6190A
OKI, racheté par Rohm, est devenu Lapis Semiconductor. Les produits se retrouvent chez Rohm semiconductor, mais ces vieux produits OKI sont introuvables sur leur site.
- [2003] OKI ML6190A datasheet
- [2005] OKI ML6190B datasheet
NPC Nippon Precision Circuits
Avec un nom pareil, NPC Nippon Precision Circuits est une entreprise japonaise, qui fait partie du groupe Seiko.
- [2004] NPC SM9501A/B datasheet préliminaire
- [2010] NPC SM9501A datasheet
- [2007] NPC SM9501B datasheet préliminaire
- [2004] NPC SM9502A datasheet préliminaire
- [2004] NPC SM9503A datasheet préliminaire
- NPC SM9507
C-MAX CMEx00x
C-MAX est une compagnie basée à Hong-Kong / Shenzhen, qui propose les puces CME6005 et CME8000 et des modules l'utilisant. C-MAX Radio Controlled Time Solution. Les puces C-MAX auraient été fabriquées par Atmel (comme les U4223B).
Puces
- [2004] C-MAX CME6005 datasheet préliminaire
- [2022] C-MAX CME6005 datasheet 2022
- [2007] C-MAX CME8000 datasheet préliminaire
Application notes
- [2006] CME6005 Application note AN001 design hints
- [2008] CME6005 Application note AN002 dual band circuitry
Modules
Ces puces sont capables d'utiliser deux bandes.
- C-MAX antenna design montre le calcul pour 77.5 kHz
Une capacité de 1.2 nF, un Q estimé à 100 (facile à faire d'après eux), une inductance de 3.5 mH, une bande passante de 0.77 kHz, et ils indiquent qu'une compensation en température sera requise, vu l'étroitesse de la bande passante...
EMAX
RCC02
Ce module utilise la puce CME6005, le câblage correspond bien à la puce. Un autre nom du module RCC02 C03A est WVB-0860N-03A.
Notez la disponibilité du signal inversé TCO sur le plot de test.
Comme beaucoup de ses confrères, une résistance R1 de 100 Ω est mise en série sur l'alimentation, ce qui évite de cramer la puce avec une surtension.
EM
Comme C-Max est un distributeur d'EM microelectronics, je soupçonne ce module d'être leur œuvre.
RC8000
Typique du module retrouvé sur des sites chinois, probablement un des plus répandus.
On les retrouve parfois sous la dénomination DCF-1060N-800 et DCF-3850M-800
La puce de réception serait la SP6007, totalement inexistante. Quand ce n'est pas le nom du module. Manifestement n'importe quoi, systématiquement recopié.
Par contre, vu le nom RC8000, et vu que c'est chinois, on peut raisonnablement penser qu'il s'agit de la puce chinoise CME8000. Mais c'est de la pure divination.
Peut-être fabriqué par QiXin jfd-ic.com : module DL8191 ?
Le module DL8362 utilise le CME6005 (qui apparait parfois en UE6005).
Silicore D6002
Shaoxing Silicore Technology a l'air d'avoir abandonné la production et le support de la puce D6002, qui devait venir de CHMC.
- [2010] Silicore D6002 datasheet
Puces / modules inconnus
Les modules dont je ne connais pas la puce d'acquisition. Ou des noms de puce suspects.
Pollin DCF1
- DCF Empfangsmodul DCF1 (site de Pollin)
- MSP430 DCF77 (Empfang und Auswertung) : contient plus d'informations techniques que la datasheet de Pollin.
BS6350 M6350
BS6350 est une puce mystérieuse, utilisée dans le non-moins mystérieux module M6350, qui n'apparait pratiquement nulle part.
- [2010] module M6350 datasheet
QiXin jfd-ic.com
Et pour finir en beauté, voici à présent le fabricant chinois mystère, mais manifestement important sur ce secteur.
QiXin www.jfd-ic.com a l'air de sévir, entre autres, dans les pendules DCF77 et consorts, proposant toute une tirée de références, vous allez être surpris, et n'oubliez pas que Google est capable de vous traduire le chinois.
À partir de la référence "8760", ce ne sont pratiquement que des modules de réception d'horloge radiopilotée ou les horloges elles-mêmes, c'est un foutoir infâme avec des centaines de références (bonne chance pour naviguer là-dedans) MAIS ils fournissent à chaque fois une datasheet certes minable.
Allez, quelques exemples :
- DL8143. Ils indiquent dans la liste qu'ils ont utilisé le MAS6181.
- module DL8362 utilise le CME6005 (qui apparait parfois en UE6005).
- module DL8306 datasheet
- module DL8191
- DL8067, DL8353, DL8330 ...
Je n'ai évidemment pas eu le courage d'essayer de comprendre et de ranger tout ça.
Si ça se trouve, c'est peut-être bien le principal fournisseur chinois pas cher de ce genre de modules, qui mange à tous les râteliers en ce qui concerne les puces.
Bonne chasse au module !