Le quantique

Un jeu à information asymétrique où les joueurs n'ont pas tous la même information a été proposé : le carré magique de Mermin-Peres.

En voici une version un poil modifiée utilisant des jetons.

• Nous avons une grille de jeu de 3 cases x 3 cases
• Alice et Bob sont chacun dans leur coin, à des années-lumière, chacun avec 2 jetons en main.
• Un arbitre désigne (au hasard) à Alice une des trois lignes : Alice peut ne rien mettre, ou placer 2 jetons, un par case, sur la ligne désignée.
• Un arbitre désigne (au hasard) à Bob une des trois colonnes, et Bob fait le même cinéma : rien ou 2 jetons.

Une fois qu'ils ont joué, on rassemble le résultat ce qui prend du temps puisqu'ils sont à des années-lumière. Alice et Bob gagne si exactement un seul jeton est placé au croisement de la ligne et de la colonne.

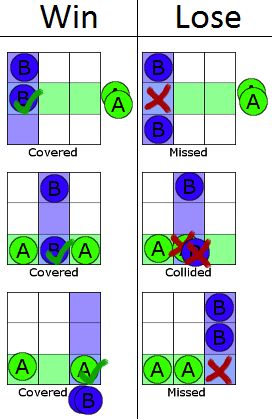
Dans le monde classique, Alice et Bob vont gagner 8 parties sur 9. Mais jamais 100%, évidemment, car il n'y n'existe pas de stratégie gagnante sans communiquer, Alice ne connait pas la colonne de Bob, et réciproquement et puis j'ai dit qu'ils étaient à des années-lumière, alors c'est difficile de communiquer.

Si Alice et Bob partagent deux paires de particules intriquées (a,b) avant d'apprendre sur quelles lignes/colonnes ils doivent jouer, alors il est possible de gagner tout le temps. En effet, on sait que si Alice lit l'état des paires de particules, alors Bob aura exactement les mêmes, et peu importe qui lit en premier, c'est le miracle de la non-localité des particules intriquées même à des années-lumière de distance.

Nos deux compères se sont mis d'accord à l'avance sur une stratégie d'utilisation des particules intriquées, avec certaines opérations quantiques logiques dépendant de la ligne/colonne désignée :

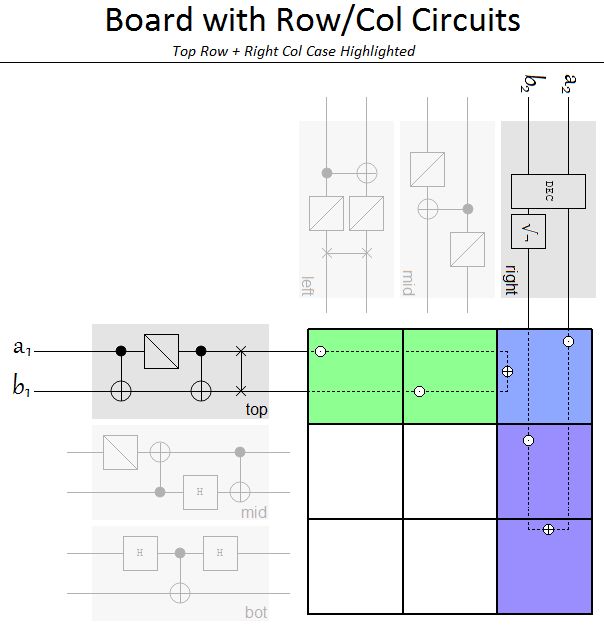
À la sortie de chaque circuit, Alice et Bob obtienne chacun 2 bits classiques d'information, qui sont évidemment corrélés grâce à l'intrication.

Alice :

• le fil du haut indique si elle doit mettre ou non un jeton sur la case à gauche
• le fil du bas pour la case centrale
• s'il lui reste un seul jeton, elle le place à droite

Bob :

• fil de gauche : case du haut
• fil de droite : case du milieu
• s'il reste un seul jeton, il le place case restante, en bas

Avec ça ils gagnent à tous les coups.

Nous avons 4 bits transmis, soit 16 combinaisons, ou encore un vecteur à 16 dimensions. Et là, c'est compliqué pour expliquer le rôle des portes si on n'a pas encore vu ça (je fais ça dans l'informatique quantique) :

http://twistedoakstudios.com/blog/Post6536_implementing-quantum-pseudo-telepathy

En court, la transformation appliquée donne une amplitude nulle aux mauvaises solutions. Les circuits proposés sont juste une solution particulière au problème, il doit y en avoir d'autres.

Cet exemple permet de comprendre comment marche la logique quantique, et des outils permettent de calculer tout ça. On remarquera qu'il faut absolument rassembler les deux informations distantes pour savoir si on a gagné : on n'ira pas plus vite que la lumière.