Intro à la mécanique quantique
Intrication

Jusqu'à présent, je vous ai pris la tête avec une seule particule.

On s'est rendu compte que la particule était capable de "voir" ce qui se passe dans l'espace, voire de "prévoir" ce qui se passe dans le temps, afin de définir son propre comportement, onde ou particule.

On a même vu que si elle se sentait "observée", alors elle n'en faisait qu'à sa tête et se montrait sous son jour "particule", mais dès qu'elle le peut, elle faisait "l'onde".

Les histoires de superposition ont l'air d'être du même acabit : déjà qu'elle peut être à la fois onde et particule, alors superposer deux états, ce n'est même plus surprenant.

À deux particules, les ennuis sont du même tonneau, voire pires.

On a vite trouvé, dans les équations mathématiques, qu'il existe une corrélation inhabituelle dans certains états dit " intriqués ", entanglement en anglais : c'est l'histoire du paradoxe EPR pour ceux que ça intéresse, et on a eu beaucoup de mal à faire la part des choses, beaucoup d'encre a coulé à ce sujet.

On va essayer de voir ça sans entrer dans des calculs fastidieux, et aussi, je ne vais pas suivre l'histoire (c'est présenté souvent comme ça), mais aller directement au problème et aux preuves.

Un dernier rappel avant de se lancer : les expériences que je décris ne sont généralement pas faciles à mettre en œuvre, mais bon, nos chercheurs ont fini par y arriver. J'éluderai les détails pratiques.

Commençons par une expérience à une particule, histoire de se remettre tout ça en tête.

Un gentil photon, possédant une polarisation P arrive sur un cube séparateur de polarisation. Si sa polarisation est parallèle au cube, il va traverser, et si elle est perpendiculaire, il va être dévié. Peu importe si c'est vertical ou horizontal, ce qui est important ici, c'est l'angle que fait le cube avec la direction de polarisation du photon.

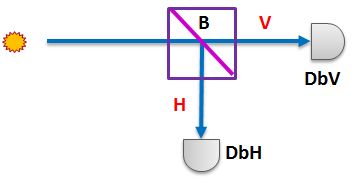
Rien de sorcier ici. Il faut juste connaitre l'angle que fait la polarisation du photon avec le cube pour savoir où il arrivera, c'est une expérience facile avec de la lumière habituelle, mais avec un seul photon, faudra bien qu'il choisisse son camp.

On va prendre un photon avec deux états superposés, et évidemment on utilise la polarisation, à la fois verticale et horizontale, et de toutes manières, il n'y a pas grand-chose d'autre avec un photon, en fait si, mais c'est nettement moins connu.

Quand le photon arrive dans le cube séparateur, il est contraint de choisir : il interagit avec les molécules du cube. Il s'engage alors d'un côté ou de l'autre. On regarde où il passe grâce aux détecteurs.

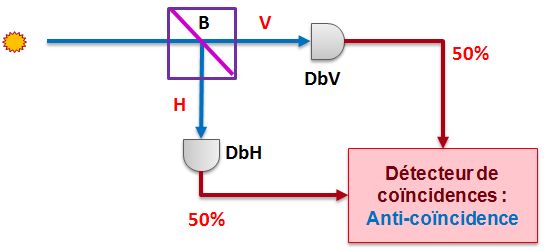
Comme on n'a rien fait de spécial avec notre photon, on connait déjà le résultat : il a une chance sur deux d'aller d'un côté ou de l'autre, et en plus, grâce à notre détecteur de coïncidence, on se rend compte qu'il n'est pas passé des deux côtés à la fois manquerait plus que ça.

Jusque-là, rien de bien surprenant. Mais vous devez me voir venir : on va dupliquer le montage et utiliser une source qui va émettre un doublet de photons (c'est l'expérience d'Aspect).

Accessoirement, c'est étonnant qu'il n'ait pas eu le Nobel, un scandale.
(Octobre 2022) Eh bien ça y est, c'est fait, Alain Aspect a eu le Nobel de physique.

Voilà un joli montage symétrique, non ? Nous avons une source de photons qui émet simultanément deux photons, l'un du côté A, l'autre du côté B.

Examinons ce qui se passerait suivant la source utilisée.

Source à un photon + lame semi-réfléchissante

Si on utilisait une source à un photon suivi d'une lame semi-réfléchissante ─au lieu d'une source à deux photons─, ce serait assez crétin : le photon irait soit du côté A, soit du côté B.

On détectera sur le côté A ou (exclusif) B, un photon soit vertical, soit horizontal, et jamais simultanément. C'est effectivement le cas. Et sans intérêt.

Deux sources indépendantes à 1 photon

Si on utilisait deux sources de photons totalement indépendantes, alors on n'aura pas de coïncidence particulière. Normal. Aussi sans intérêt.

Source à un photon + convertisseur bas

Quand on utilise une paire de photons créés à partir d'un seul (grâce au coup du convertisseur bas), on observe le résultat suivant en coïncidence (le montage est parfaitement symétrique) :

• Soit {VA, VB} : ils traversent le cube tous les deux, ils sont verticaux
• Soit {HA, HB} : ils sont réfléchis tous les deux, ils sont horizontaux
• Mais JAMAIS horizontal d'un côté et vertical de l'autre

Et en plus, on sait, grâce au détecteur de coïncidences, qu'il s'agit bien du couple initial. Pas de lézard, ils ne se sont pas perdus en route.

On dit alors que les deux photons sont intriqués.

• Si on mesure A en premier, quand on va mesurer B, alors, B aura la même polarisation que A.
• La situation est symétrique : le premier qui mesure " gagne ".

Et ça, c'est magique. Parce que ça ne dépend pas de la distance. Les deux détecteurs peuvent être à des années-lumière l'un de l'autre, on aura toujours cette corrélation, dixit la mécanique quantique.

Ça ne parait pas encore trop délirant après tout : les deux photons sont frères, ils sont dans le même état, normal qu'ils fassent pareils, non ? Mais c'est quand même bizarre, car chaque photon est dans un état superposé, autrement dit chacun ne sait pas encore "qui il est".

• Mais bon, ils se sont peut-être mis d'accord sur une variable cachée commune au départ, variable qui déterminerait leur comportement ?
• Ou alors c'est le premier, qui envoie une information (non locale) à l'autre, plus vite que la lumière ?
• Quelqu'un a une autre idée ?