Intro à la mécanique quantique
Incertitude et superposition

Première remarque : on a des ondes, alors on peut les additionner. Par exemple, on peut avoir une onde polarisée horizontalement + une onde polarisée verticalement. Si la valeur du champ est identique pour les deux, on se retrouve avec une onde circulaire à 45 degrés.

On a alors un truc qui ressemble à de la superposition. Mais ce n'est pas de la superposition au sens quantique, c'est juste que l'axe est tourné de 45 degrés par rapport à votre référence.

Un photon peut avoir les deux polarisations, horizontale et verticale, en même temps comme dirait Macron.

C'est assez déroutant car on pourrait se dire qu'en fait, il est simplement à 45 degrés, la combinaison des deux.

Mais non, il a réellement les deux à la fois, on constate ça par déduction, on verra plus tard.

Un truc déroutant, c'est que c'est toujours par rapport à une référence que vous choisissez, vous: mais comment le photon le sait-il ? Il doit trainer un truc relativiste quelque part, qui n'a jamais été exhibé.

C'est peut-être plus simple à comprendre avec le spin des électrons, car on les regarde rarement comme une onde.

On a découvert que les électrons avaient une propriété particulière en plus de leur charge et de leur masse : le spin.

On se le représente souvent comme une sorte de toupie dont l'axe peut être dirigé vers le haut ou vers le bas, parce qu'on pense que cela est lié au moment cinétique propre (rotation sur lui-même, si cela a un sens).

Le petit film suivant présente bien ce phénomène : inutile que je m'enquiquine à refaire ce qui est bien.

En fait, il n'y a pas que les électrons qui ont un spin s, ce sont toutes les particules.

L'électron, le proton et le neutron ont un spin ½, le photon un spin 1, les mésons p un spin 0, etc.

Le truc étonnant, c'est que cette valeur est quantifiée : c'est toujours un multiple entier ou demi-entier de la constante de Planck réduite (h/2π) : il ne peut en exister que 2s + 1 pour un spin s ; ainsi, le spin de l'électron ne peut prendre que 2 × ½ + 1 = 2 orientations, c'est ½ ou -½.

Les fermions sont des particules de spin ½. Ils ont la particularité de ne pas pouvoir avoir exactement le même état physique individuel = ils doivent être tous différents (c'est le principe d'exclusion de Pauli). Ce n'est pas le cas des bosons, les particules de spin entier, qui peuvent avoir un comportement collectif, tous identiques.

Cette histoire d'orientation est quand même bizarre : on peut " voir " le spin uniquement dans des conditions particulières, par exemple dans un champ magnétique, et c'est lui qui donne l'orientation vous choisissez, vous avez ce super-pouvoir. Quand il n'y a pas de champ, on peut se demander ce que c'est… et de toute façon, sans champ magnétique, il n'y a rien à voir, alors, circulez. Mais bon, pourquoi pas ?

Après tout, notre électron peut bien avoir une orientation, qui devrait suivre en toute logique certaines règles du genre "moi, j'ai cette orientation, toujours la même". C'est d'ailleurs un peu ce qui se passe en électronique de spin ou spintronique : on a quand même une nette tendance à vouloir sélectionner l'orientation de nos électrons avec des ruses diverses pour s'en servir plus tard.

Voilà, on arrive enfin au fait.

Et ben non, on s'est rendu compte que l'électron pouvait avoir les deux états de spin à la fois, superposés, en même temps redirait Macron.

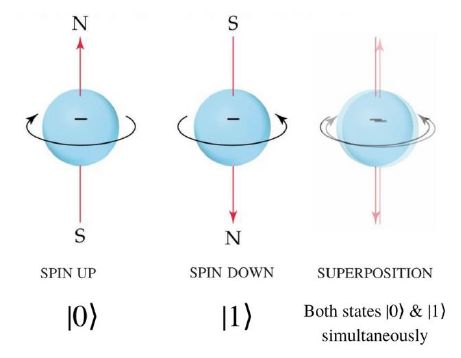
Comment peut-on démontrer un truc pareil ?

En effet, je ne vois rien tant que je ne mesure pas, et quand je mesure, forcément qu'un seul des deux est vu, mais bon, c'était peut-être déjà comme ça initialement !

On l'a démontré dans cette expérience: bis repetita: inutile que je m'enquiquine à refaire ce qui est bien.

Et puis dans d'autres expériences, on finit par se dire que c'est forcément comme ça. De toutes manières, cette histoire de superposition est une conséquence mathématique d'une équation dont on n'a pas d'autre démonstration que de constater qu'elle marche…

Dans le bout film précédent, vous avez vu une histoire de décohérence : l’état quantique de superposition est perdu au bout d’un moment, essentiellement à cause des interactions inévitables avec l’environnement. Dans l’air à température ambiante, on a mesuré 10^-17 seconde.

C’est court.

Très court.

Gênant pour faire une mémoire quantique...

D’où les travaux et ruses diverses pour contourner ça, le plus connu étant d’aller vers le zéro absolu. Mais ce n’est pas commode.

Quand on veut lire une grandeur physique, forcément qu’on est obligé d’utiliser un instrument de lecture « physique », et donc on vient aussi perturber l’état quantique du truc qu’on veut mesurer. On dit que la fonction d’onde s’effondre, et on obtient uniquement un état réduit, avec une certaine probabilité pour avoir l’une ou l’autre des valeurs superposées. Une sorte de décohérence aussi, mais voulue cette fois.

Vous entendrez beaucoup reparler de ça quand on discutera qubit. Parce que dans l’ordinateur quantique, à un moment ou à un autre, faudra bien lire le résultat dans le monde classique, sinon ça ne servira pas à grand-chose.