Chiffrement RSA
C'est quand même curieux cette histoire de factorisation infaisable en pratique, alors qu'il faut générer deux nombres premiers : comment fait-on pour savoir s'ils sont premiers sans factorisation ?
Autant vous prévenir tout de suite, vous ne trouverez ici qu'un résumé des principaux points à connaitre concernant le chiffrement RSA, vu qu'il existe des centaines d'autres descriptions que vous trouverez en cherchant un tant soit peu sur le web.
Je n'ai par contre pas esquivé certains détails polémiques 😁
Le chiffrement RSA, proposé en 1977, fait partie des algorithmes de chiffrement dit asymétriques : vous pouvez publier votre clé publique pour que n'importe qui puisse vous envoyer un message secret.
Algorithme
Voici la méthode à suivre pour réaliser un chiffrement RSA :
- Choisir p et q, 2 grands nombres premiers
sensiblement de même taille (voir plus loin la raison) - Calculer le produit n = p * q
on l'appelle parfois nombre semi-premier - Calculer la fonction d'Euler de n : Φ(n) = (p-1) * (q-1)
fait bien dans la conversation, surtout si on ajoute que la fonction d'Euler donne le nombre d'entiers premiers avec n - Choisir e tel que 1 < e < Φ(n)
et e premier avec Φ(n)
e est aussi appelé exposant de chiffrement - Calculer d tel que d * e ≡ 1 modulo Φ(n)
modulo k ou mod(k) veut simplement dire "reste de la division par k"
Vous avez alors :
- Une clé publique : le couple (e,n)
- Une clé privée : le couple (d,n)
Chiffrement
Avec la clé publique (e,n), on chiffre le message m :
m doit être un nombre inférieur à n.
c est le "chiffré".
On voit tout de suite qu'il faudra être plus malin car avec cette méthode seule, le même message donnera toujours le même chiffré.
Pour éviter ça, on introduira « du sel », un aléa (qui sera transmis) de manière à obtenir un message chiffré différent pour le même message d'entrée. C'est une technique courante et obligatoire.
Déchiffrement
Avec la clé privée (d,n), on déchiffre le message chiffré c :
Exemple
Voici un exemple pour voir l'étendue des dégâts concernant les calculs.
- On choisit p=61 et q=53
- On calcule n = p * q = 61 x 53 = 3233
- On calcule Φ(n) = (p-1) * (q-1) = 60 x 52 = 3120
- On choisit e = 17.
Comme le PGCD(17,3120)=1, il est bien premier avec Φ(n)
Algorithme d'Euclide
- Diviser 3120 par 17 (3120 = 17x183 + 9) : le reste vaut 9
- Recommencer pour le diviseur 17 et le reste 9 (17 = 1x9 + 8) : il reste 8
- Recommencer pour le diviseur 9 et le reste 8 : il reste 1
- Recommencer pour le diviseur 8 et le reste 1 : il reste 0
Le dernier diviseur avec le reste 0, ici 1, est le PGCD.
Comme le PGCD vaut 1, 3120 et 17 sont premiers entre eux.
- Il faut résoudre l'équation d * e ≡ 1 modulo Φ(n)
soit d * 17 ≡ 1 modulo 3120 : on trouve d = 2753
Algorithme d'Euclide étendu
Trouver d tel que :
L'équation suivante est plus simple à comprendre que ces notations mathématiques que vous avez oubliées. Il faut trouver d et k tels que :
Or l'identité de Bézout est reliée au PGCD :
On commence par trouver le PCGD entre 17 et 3120, vu ci-dessus. Il vaut 1, cela veut dire que l'inverse existe. Avec la liste des restes, 1, 8, 9 puis 17, on va pouvoir "remonter" les combinaisons linéaires :
or on a vu lors du calcul du PGCD que 8 = 17 - (1*9) d'où
or on a vu lors du calcul du PGCD que 9 = 3120 - (183*17) d'où
On a trouvé d=-367 et accessoirement k=2. Comme d est négatif, on ajoute le modulo 3120 pour obtenir un nombre positif 2753.
On dit que l'inverse de 17 (1 divisé par 17 si vous voulez) modulo 3120 est 2753
Nous avons alors :
- Clé publique : le couple (17,3233)
- Clé privée : le couple (2753,3233)
Pour chiffrer m = 65 (qui respecte la condition « inférieur à 3233 ») :
Et pour déchiffrer c :
Exponentiation rapide
Calculer 27902753 modulo 3233
Il ne faut pas calculer 27902753, mais remarquer que :
Autrement dit, il suffit de multiplier uniquement le reste, ce qui va éviter des nombres vraiment astronomiques.
Mais ce sera quand même assez long.
Sécurité
Chiffrement
Casser un seul message n'est généralement pas très intéressant, surtout si le coût de décryptage est élevé.
S'il faut tout recommencer du début pour le message suivant...
Vaut mieux essayer de trouver la clé de chiffrement.
Trouver la clé
Casser RSA
Beaucoup de gens tentent de casser RSA, vous trouverez beaucoup de documentation sur le web.
- [2004] Conception et preuves d’algorithmes
cryptographiques / ENS / Jacques Stern, Louis Granboulan, Phong Nguyen, David Pointcheva
Document qui peut paraitre ancien, mais pas tant. Le chapitre 3 est consacré à toutes les attaques de RSA. C'est à peu près lisible et vous y trouverez des détails sur certaines techniques d'attaques comme « l'attaque à chiffré choisi ».
Vous verrez qu'il existe des attaques nettement plus subtiles que de tenter de factoriser.
Factoriser
Cela fait longtemps que bon nombre de personnes essayent de trouver des méthodes de factorisation, et il n'en existe pas tant que ça, et elles ne marchent pas sur des grands nombres. D'ailleurs il existait un challenge pour factoriser des nombres semi-premiers de plus en plus grands.
- RSA Factoring Challenge / Wikipédia
RSA numbers (liste de nombres à factoriser)
En 2025, on était rendu à 829 bits (RSA-250), qui date de 2020, avec 2700 années-CPU.
Il est courant d'entendre qu'une clé de 2048 bits est conseillée actuellement, pour être peinard jusqu'en 2030. Après, par prudence, il vaudra mieux augmenter la taille, le coût étant du temps de calcul supplémentaire ce qui ne parait pas vraiment un problème.
Factorisation
Méthode algébrique
Il s'agit des méthodes mathématiques pour factoriser.
- La plus triviale est la méthode des divisions successives.
- La méthode de Fermat
- La méthode de Gauss
- La méthode p-1 de Pollard
- La méthode ρ de Pollard
- La méthode des factorielles
- Le crible quadratique (et la machine de Carissan)
- La méthode ECM de Lenstra (courbes elliptiques)
- Le crible du corps des nombres
- ...
Bon courage à ceux qui veulent creuser toutes ces méthodes, j'ai mis quelques documents en référence à la fin pour démarrer vos recherches.
Actuellement, la plus rapide est la méthode du crible algébrique (Number Field Sieve ou GNFS en anglais). Et pour donner un ordre de grandeur, pour factoriser un nombre de 2048 bits, il faudrait :
- Bien plus de 10³⁴ années avec une bonne machine actuelle
- 10¹⁶ années en optimisant les choses sur du matériel dédié avec des puces ad-hoc.
Les durées ne sont probablement pas très précises, et même avec plusieurs décades d'erreur, ce qu'il faut retenir, c'est que ce sont des temps vraiment astronomiques.
Algorithmes génétiques
Tout part de la remarque que nos chromosomes se dupliquent et se combinent avec des mutations, et que la sélection naturelle ne conservera que les "meilleurs", plus exactement ceux qui sont les plus adaptés.
Alors on s'est dit qu'on pourrait peut-être en prendre avantage pour résoudre des problèmes où la combinatoire explose. Sauf qu'il va falloir être malin pour "évaluer chaque individu d'une population de chromosomes", et donc définir des fonctions adaptées au problème posé.
Pour le moment, cette méthode semble inadaptée pour la factorisation. Je l'ai citée anecdotiquement, par complétude, si quelqu'un y pense.
Intelligence artificielle
Certains essayent de factoriser à l'aide de l'intelligence artificielle, ou plutôt de l'apprentissage profond.
Dis comme ça, ça m'étonnerait que cette méthode mène quelque part, vu que l'IA est juste capable de vous ressortir
ce que vous connaissez déjà...
On appelle ça un consultant dans les entreprises, qu'on paye très cher.😁
Calcul quantique
Il existe deux manières d'utiliser les qubits pour effectuer une factorisation (ainsi que d'autres calculs) :
- La manière que l'on peut qualifier de traditionnelle, où on exécute des portes quantiques, et dans le cas de la factorisation, il s'agit de l'algorithme de Shor. Si vous n'y connaissez rien en ordinateur quantique, il vaut mieux démarrer par le début. Vous verrez que j'ai détaillé le fonctionnement par le menu.
- L'autre manière est ce que l'on peut appeler les ordinateurs adiabatiques comme ceux de D-Wave, une méthode de recherche de minima par recuit simulé, voir ci-après.
En quelques mots, Shor a trouvé le moyen de transformer le problème en une recherche de période grâce à une astuce mathématique, que je détaille dans une de mes pages.
Or un ordinateur quantique est très fort dans cet exercice à l'aide de la transformée de Fourier quantique.
Pour l'algorithme de Shor, on parle au bas-mot de millions de qubits requis. En 2025, on en est encore dans les centaines pour les puces disponibles, et encore, les jours de beau temps car ces bestioles sont très susceptibles côté bruit, j'en ai fait l'expérience moi-même.
Mais si ça marche, on parle de jours pour factoriser un nombre de 2048 bits. Rien à voir avec les millions de milliards d'années avec nos moyens de calculs classiques.
- [2021] Factoring 2048-bit RSA Integers in 177 Days with 13 436 Qubits
and a Multimode Memory / Élie Gouzien & Nicolas Sangouard
Comme réaliser beaucoup de qubits vraiment fonctionnels semble être un challenge délicat, certains essayent d'économiser en utilisant des mémoires et interfaces ad'hoc. - [2019] How to factor 2048 bit RSA integers in 8 hours using 20 million noisy qubits / Craig Gidney, Martin Ekerå
Calcul adiabatique
Il s'agit des méthodes du genre « recuit simulé », où on s'arrange pour transformer le problème en une recherche de minimum d'énergie. En baissant doucement la « température » du système, on espère alors parvenir à ce minimum, sachant qu'il peut exister des minima locaux qui gêneront cette recherche. J'explique cela dans une page spéciale sur le recuit simulé et consorts où j'ai pris la factorisation comme exemple.
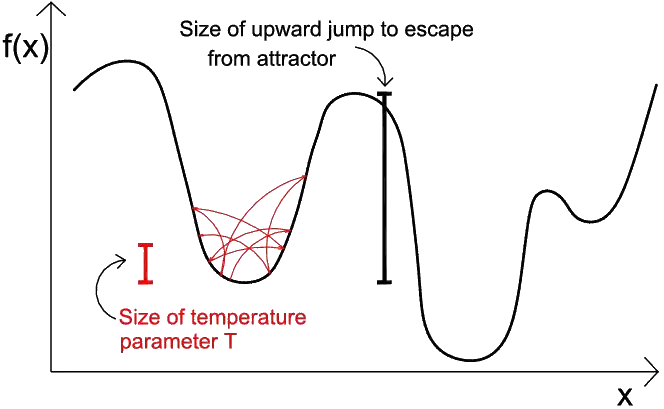
Outre le calcul direct classique, il existe au moins deux types de machines permettant cette recherche :
- Les ordinateurs quantiques. On parle alors de « quantum annealing », c'est ce que les ordinateurs de D-Wave proposent.
- Les systèmes reposants sur ce qui est appelé les p-bits, les bits probabilistes, qui évoluent entre 0 et 1.
Comme il s'agit d'un sujet un peu compliqué, et qui pourrait s'appliquer en remplacement du calcul brutal réalisé par les ordinateurs en ce qui concerne l'intelligence artificielle, j'ai réalisé une page plus détaillée qui reprend en partie mes vieilles explications pour expliquer comment ça marche et le gain apporté.

Générer des nombres premiers
Test de primalité
Les tests de Solovay-Strassen et Miller-Rabin sont des algorithmes probabilistes qui vous diront que "n est probablement premier" avec une probabilité que l'on peut ajuster. Autrement dit, on sait faire des tests pour montrer qu'un nombre n'est pas premier, et quand on ne trouve pas, on dit qu'il est probablement premier.
L'idée est la suivante (et c'est juste pour effleurer le sujet, c'est plus compliqué que ça) :
- Supposez que vous avez un test qui, pour un certain paramètre "a", vous dise qu'un nombre n'est pas premier.
- De plus, vous savez que ce test a une chance sur 2 de passer, parce que vous connaissez la proportion de nombres premiers parmi les entiers naturels (par exemple un nombre de 1024 bits a une chance sur log(2¹⁰²⁴) ≈ 710 d'être premier).
- En essayant 32 fois (avec 32 "a" différents), vous aurez une chance sur 2³² soit 4 milliards qu'il ne soit pas premier.
En pratique, la probabilité d'erreur est majorée par ¼, et on fait 50 tests, soit 2¹⁰⁰
Reste à espérer que ce soit correctement codé...
Documentation
Vous trouverez pas mal d'articles et de documents sur le web à propos des mathématiques appliquées à RSA, le principal problème étant que c'est généralement confus, incomplet, peu clair. En voici quelques-uns, en français, qui m'ont paru plus intéressants.
- [2014] Notes du cours PO-13502
Cryptage RSA et tests de primalité / B. Ischi
Plutôt bien écrit et relativement complet. Avec des exemples de codes et d'exécution. - [2018] Arithmétique et Tests de Primalité
/ Pierre Rouchon
Si vous préférez une présentation sous forme de planche. - RSA, Primalité, Factorisation / Martin WEIMANN
Un autre document mathématique, moins complet. - [2009] Chapitre V -
Tests et critères de primalité / Alain Kraus
Les mathématiques concernant les tests de primalités. Assez complet à première vue. - [1998] La factorisation des grands nombres
/ Johannes Buchmann
De la vulgarisation, on y trouvera la «machines à congruences» de l’officier français Eugène Carissan - [2014] La factorisation des grands nombres
/ Accromath volume 14
Un dossier de vulgarisation vraisemblablement plus accessible. Inclus un historique, les algorithmes génétiques...
À mon avis, il n'y a pas lieu de s'inquiéter à propos de la longueur de clé. Si l'ordinateur quantique marche un jour, il faudra changer d'algorithme de chiffrement.
De toutes manières, si quelqu'un réussit à trouver une méthode de factorisation, elle ne sera pas publiée mais classifié par l'État et ses militaires...