Recuit simulé, machine d'Ising, p-bits...
La situation est confuse lorsque l'on commence à aborder le sujet du recuit simulé,
des machines d'Ising, des bits probabilistes dits p-bits, des ordinateurs adiabatiques ou thermodynamiques,
et autres joyeusetés. C'est le boxon.
Et c'est pareil en anglais, sauf que là, c'est le mess.
Et en plus, ce serait censé résoudre le problème énergétique posé par l'IA et ses data centers monstrueux.
De quoi parle-t-on ?
Si la situation est simple du côté informatique pour l'exécution d'algorithmes classiques, et à peu près aussi simple à décrire, pas à comprendre pour les algorithmes quantiques sur machines quantiques "universelles", il existe d'autres solutions pour résoudre des problèmes souvent particuliers, basées quasiment toutes sur la recherche de minima par des moyens détournés, sans calcul direct. C'est de ça dont on va parler.

Un problème très similaire est celui du voyageur de commerce.
Perso, quand j'étais petit, je résolvais le problème avec des bulles de savon :
La nature, ici la tension superficielle, par sa fainéantise bien connue, cherche la solution énergétique la plus faible.
L'idée consiste à transformer le problème en un minimum à trouver sur une machine qui sera spécialement conçue pour ça.
Recuit simulé, adiabatique, thermodynamique...
Dans le temps, on avait la technique du recuit simulé (simulated annealing) pour trouver un minimum, en fait on recherchait un état minimal d'énergie, une chose que la nature fait très bien naturellement, même quand il existe des minima dits locaux. On dit recuit simulé parce qu'on fait lentement baisser la température pour trouver le minimum, tout en gardant une certaine agitation thermique histoire de pouvoir franchir un col afin de découvrir le trou le plus profond.
Retenez que de l'aléatoire est introduit, souvent via du bruit.
Mais l'agitation thermique va introduire des variations aléatoires permettant de franchir un col.
Comme on parle de température, on utilise parfois (souvent ?) le terme thermodynamique, ce qui permet d'impressionner les foules.
Mieux, les machines utilisant ce genre de technique sont parfois affublées du terme « adiabatique » qui fait bien dans la conversation. Stricto sensu, cela signifie qu'il n'y a aucun échange de chaleur (d'où le lien avec la température).
Cela peut être perçu ainsi : vous avez un pendule qui oscille. Si vous déplacez très lentement le pendule, vous ne verrez quasiment pas de changement par rapport à son support, il oscillera pareil. Mais si vous bougez trop vite (= non adiabatique), et bien vous mettez la zone dans le mouvement.
Quantique abiabatique
On n'utilise pas stricto sensu la température dans tous les appareils qui vont permettre de trouver un minimum, il s'agit juste d'une représentation. C'est pareil pour l'énergie qui devient une analogie au sens large et permet de savoir de quoi on parle dans le meilleur des cas.
Et puis ça ne se limite pas à une seule dimension, on est rapidement mis en face de multiples dimensions, surtout lorsqu'il existe de multiples facteurs.
Notez les techniques de franchissement.
Si l'agitation thermique permet de franchir un col local, il est possible d'utiliser aussi l'effet tunnel, un effet qui n'existe que dans le monde quantique.
C'est un des effets recherchés dans les ordinateurs quantiques dits adiabatiques, autrement dit les ordinateurs à D-Wave pour citer la compagnie la plus connue sur ce terrain. L'autre effet étant l'intrication, autrement dit ces espèces d'interactions à distance entre qubits, également utilisée dans les ordinateurs quantiques normaux ou universels.
Discrétisation
Jusqu'à présent on se représente cette histoire de recherche de minimum par une gentille fonction continue, éventuellement sur plusieurs dimensions ou paramètres, que l'on parcoure.
Le monde étant devenu ce qu'il est, digital et en plus quantique, on est rapidement allé vers des solutions où on manipule des petits objets reliés entre eux par des fonctions (ou des coefficients pour les cas simples). C'est déjà le cas pour les ordinateurs quantiques adiabatiques qu'on vient d'évoquer, où on utilise des qubits, plus ou moins bien reliés entre eux.
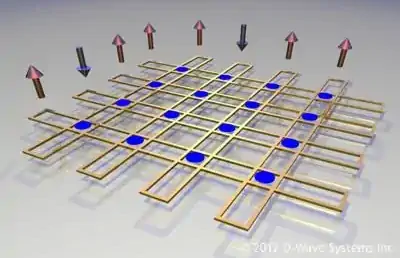
Machine d'Ising
Cette discrétisation peut se généraliser sous la forme d'une machine d'Ising : vous avez un réseau de nœuds reliés par des poids décrits dans une fonction appelée « hamiltonien ».
On peut voir ça comme une boucle qui va s'exécuter tant que le minimum (où plus rien ne bouge) n'est pas atteint. Cette façon permet de réutiliser les mêmes nœuds physiques.
Mais on peut aussi voir ça comme une séquence avec des "plans de nœuds" successifs, comme une matrice de neurones qui seront reliés par des poids, et là on fait le lien avec la fameuse intelligence artificielle, qu'on devrait plutôt appeler « apprentissage profond ».
- [2022] Ising machines: Hardware solvers for combinatorial
optimization problems / Mohseni & al.
Vous verrez que la situation est bien plus compliquée que la simplification drastique que je vous présente. - [2024] A Review
of Ising Machines Implemented in Conventional and Emerging Technologies / Tingting Zhang & al.
- Un livre de référence, si vous voulez creuser le sujet :
[2023] Probabilistic Machine Learning : Advanced Topics / Kevin Patrick Murphy. Bon courage !
Types de nœuds
Concernant les nœuds, les chercheurs sont très imaginatifs.
Voici une classification à l'emporte-pièce, ce sera mieux que rien :
- Les bits : bien connus, uniquement 0 ou 1, on revient aux calculs classiques.
- les p-bits : les bits probabilistes. Les nœuds présentent une valeur réelle entre 0 et 1.
- les qubits : ordinateurs quantiques de type adiabatiques. Les nœuds présentent des valeurs complexes (avec nombres imaginaires)
- les s-units : la version analogique, histoire de ne pas les oublier, il n'y a pas que le digital dans la vie.
Retenez deux points importants :
- Les nœuds présentent un certain bruit, ils sont aléatoires, mais on peut régler la distribution de probabilité (dans le meilleur des cas). Du bruit thermique, du bruit quantique, ce que vous voulez, il existe beaucoup de propositions.
- Les nœuds sont reliés entre eux par des fonctions ou plus simplement des coefficients. Mais chaque nœud n'est pas forcément relié à tous les autres nœuds, ça va dépendre des machines, et cela aura un impact énorme sur les performances.
Exemple
Voici un exemple relativement simple d'une machine d'Ising basée sur 80 jonctions tunnel superparamagnétiques (SMTJ), qui sont toutes interconnectées, machine capable de trouver le chemin le plus court d'un voyageur de commerce visitant 70 villes.
Une jonction tunnel de ce type présente deux états de spin (parallèle P et antiparallèle AP), que l'on obtient aléatoirement avec une distribution qui dépend du courant injecté :
La résistance de la jonction est variable au cours du temps, la jonction oscille entre les deux états de spin, avec une probabilité qui dépend du courant injecté :
Vous pouvez voir ça comme un générateur de nombres aléatoires TRNG
dont on peut contrôler la distribution de 0 et de 1.
Nous voici donc avec 80 jonctions dont on peut régler la distribution de probabilité entre deux états (ici P et AP, 0 et 1 si vous préférez). La mise en œuvre est directe :
- La lecture de l'état de chaque jonction se fait avec un comparateur (il en faut 80)
- Les états lus sont transférés à un microcontrôleur (MCU)
- Le microcontrôleur peut alors calculer, suivant des règles à programmer en fonction du problème posé, une nouvelle liste de 80 distributions à appliquer pour le tour suivant.
- Un DAC (un convertisseur digital vers analogique) convertit chaque valeur de distribution désirée vers le courant correspondant.
- Les jonctions vont alors se mettre à osciller entre les deux états, et à un moment donné, on lira leur état, qui sera aléatoire.
Dans ce cas précis, avec une telle architecture, chaque jonction peut dépendre de toutes les autres jonctions, ce qui est bien évidemment favorable pour la résolution des problèmes.
Avec n=80 jonctions, ça nous fait (n-1)n/2 soit 3160 coefficients à gérer. Ça passe facilement avec un microcontrôleur.
Le papier explique comment le problème du voyageur de commerce est programmé dans cette machine : il faut convertir le problème et ses paramètres en une série de coefficients.
Pour 9 villes, la machine commence à converger en 50 itérations, et il lui faut quelques milliers d'itérations pour trouver la solution. Normalement, pour résoudre le problème du voyageur de commerce à N villes, il faudrait (N-1)² spins. Pour trouver la solution à 70 villes, les auteurs ont découpé le problème en morceaux et fait glisser une fenêtre. Environ 400 000 itérations requises.
Si les calculs à réaliser entre chaque itération va avec le carré du nombre de jonctions, la consommation électrique pour trouver la solution est indéniablement extraordinairement basse comparée aux méthodes algorithmiques habituelles sur CPU.
Limitation physique
Dans l'exemple précédent, les interactions entre les nœuds est assurée par les calculs du microcontrôleur, c'est lui qui va prendre cher quand on augmentera le nombre de bits.
Mais on peut aussi avoir des nœuds qui soient directement reliés entre eux. On se doute que cela pourrait marcher pour des nœuds voisins, topologiquement parlant. Mais si deux nœuds sont éloignés, ça va moins bien se passer. Sauf pour les qubits (qui présenteront d'autres problèmes) : on sait qu'ils peuvent interagir à distance.
On se doute qu'à un moment où à un autre, on va associer un nœud à un bit d'information à trouver, par exemple chaque chiffre binaire d'un grand nombre, et les liens entre chaque nœud seront importants, voire impératifs, sinon ça ne marchera pas. Ce qui veut dire que la complexité du problème va croitre rapidement avec le nombre de nœuds (le carré dans l'exemple), et vous ne pourrez pas implémenter physiquement une machine avec beaucoup de nœuds, elle sera vite limitée.
C'est ce qui arrive pour toutes les machines proposées par certaines compagnies pour résoudre les problèmes d'énergie et de temps de calcul. Départ arrêté, sur le papier, ça fonctionne, et d'ailleurs ils le montrent pour des "petits nombres", mais ils ne peuvent pas faire fi de l'explosion combinatoire qui se présente lorsque le nombre de bits/paramètres augmente. Ils ne pourront résoudre que certaines classes de problèmes.
Et certainement pas les problèmes et calculs de l'intelligence artificielle qui manipule bien plus que quelques centaines de misérables bits.
Factorisation
Transformation du problème
Voici un exemple pratique de transformation de problème en une recherche de minimum, à la portée de tout un chacun.
Pourquoi la factorisation ? Car pouvoir factoriser un grand nombre signifierait la fin du chiffrement RSA ses carottes seraient... cuites.
Il s'agit de transformer le problème de la factorisation en un jeu d'équations qui concerne chaque chiffre (binaire) des deux nombres premiers à trouver. L'article de Microsoft de 2002 Factoring as Optimization montre un exemple avec 91=13*7.
Soient x et y, deux nombres premiers qui donnent N = xy.
x et y sont forcément impair et finissent par 1 sinon il y aurait 2 comme facteur premier, c'est con.
Il suffit de poser la multiplication à l'ancienne, comme appris à l'école mais en binaire :
Et on se retrouve avec un magnifique jeu de 7 équations, en faisant gaffe aux retenues introduites avec z :
Il faut alors éliminer des variables, tirer parti du fait qu'il existe deux solutions symétriques (xy ou yx) pour simplifier les équations.
L'astuce consiste alors à ne pas se limiter à deux valeurs entières (0 et 1), mais à rendre les fonctions continues, et alors cela revient à rechercher un minimum avec des nombres réels.
Injection dans une machine d'Ising
Ensuite, il faut coder ces équations de factorisation de manière à rentrer dans votre machine d'Ising, ou votre algorithme de recuit simulé. Pas mal de tentatives ont été proposées, en voici quelques-unes (trouvées au hasard de mes recherches, ce n'est certainement pas exhaustif) :
- [2014 / 2021] Using Simulated Annealing to Factor Numbers
/ Eric Lewin Altschuler and Timothy J. Williams
Recuit simulé très basique, et sans résultats vraiment intéressant. Juste pour embêter RSA. - [2016] Prime factorization using quantum annealing
and computational algebraic geometry / Raouf Dridi & Hedayat Alghassi
Une variante qui pourrait simplifier un peu les choses, d'un intérêt relatif. - [2018] Quantum Annealing for Prime Factorization
/ Shuxian Jiang & al.
Pour montrer le bien-fondé de la solution D-wave - [2020] Prime factorization algorithm based
on parameter optimization of Ising model / Baonan Wang & al.
Pour montrer le bien-fondé de la solution D-wave - [2023] E-Spin: A Stochastic Ising Spin Based on Electrically-Controlled MTJ
for Constructing Large-Scale Ising Annealing Systems / Wenhan Chen & al.
64 E-spins et nombres de 64 bits factorisés. - [2024] Rydberg-atom experiment for
the integer factorization problem / Juyoung Park & al.
démonstration sur des petits nombres - [2024] Effective prime factorization
via quantum annealing by modular locally-structured embedding / Jingwen Ding & al.
Utilise le matériel D-Wave, aussi pour enquiquiner RSA. Vous reconnaitrez la décomposition en équations. - [2025] General integer factorization algorithm based on
Ising machine / Zhang Luo & al.
entier de 22 bits factorisé avec 118 qubits. D-wave. - [2025] Highly
durable and energy-efficient probabilistic bits based on h-BN/SnS 2 interface for integer factorization / Joon-Kyu Han & al.
Ressemble beaucoup à la machine d'Ising présentée ci-dessus en exemple. Détaille comment la factorisation est intégrée avec un exemple simple à 4 bits. Affirme qu'un réseau de 2716 p-bits pourrait factoriser les 2048 bits d'RSA, ce qui me parait très optimiste. - [2025] A First Successful Factorization of RSA-2048 Integer
by D-Wave Quantum Computer
Je vous laisse trouver l'entourloupe. - Le simulateur web de l'université de Purdue concernant une factorisation avec des p-bits (Purdue grenouille dans ce domaine depuis des lustres) : 8-bit factorizer
Comment dire ? Ça, ça cherche, surtout chez D-wave qui publie pour continuer à obtenir de l'argent. Mais ça ne trouve pas vraiment. Quand on arrivera à factoriser un nombre de 2048 bits, ça se saura vite. Ou plutôt non, l'État et l'armée étoufferont l'affaire.
Machines
On parle essentiellement de deux types de machines concernées par ces méthodes :
- Les ordinateurs quantiques adiabatiques, comme ceux de D-wave.
- Les machines basées sur les bits probabilistes, comme celles proposées par l'université de Purdue.
Les deux implémentent un modèle d'Ising plus ou moins visible.
- Pour les p-bits, il s'agit d'une exploration "thermique", avec du bruit stochastique pour l'introduction des aléas.
- En ce qui concerne les qubits, l'exploration se fait par "tunnel quantique", éventuellement avec l'aide de l'intrication. Les aléas sont du "bruit quantique" si tant est qu'on arrive à définir correctement cela (c'est l'environnement thermique (pff !) qui met la zone en provoquant de la "décohérence").
Réflexions sur les calculs
Calcul quantique
Si vous avez lu un peu ma présentation sur les ordinateurs quantiques, vous avez dû remarquer que je considère ces machines comme étant de simples machines à calculer capable uniquement de multiplier des matrices de nombres complexes. Et que nous avions des limitations très sévères :
- incapable de rentrer ce qu'on veut comme nombres complexes, uniquement quelques opérations assez basiques.
- incapable de lire les nombres complexes de la matrice, on est obligé de passer par une réduction de la fonction d'onde qui ne donne qu'une information partielle, il faut alors répéter le calcul pour obtenir un peu de statistique
Et ne vous laissez pas avoir par les histoires de superposition et d'intrication : ce ne sont que des représentations mentales pour essayer de comprendre ce qui se passe, ces pseudo-phénomènes ne sont que la traduction des variations des valeurs dans la matrice. Par exemple, l'intrication n'est que la traduction de la non-factorisation de la fonction d'onde. Eh oui, tout se passe dans la multiplication.
D'ailleurs, lorsque l'on veut simuler un système de qubits, on passe son temps à multiplier des matrices carrées de la taille du nombre de qubits, ce qui devient rapidement bien trop gros pour n'importe quel ordinateur.
Calcul conventionnel
Puisqu'on en parle, les calculs conventionnels sont limités par :
- le temps de calcul d'une opération
- le nombre de processeurs disponibles
En oubliant les problèmes énergétiques et d'évacuation de chaleur.
Si on compare avec le calcul quantique, c'est vexant car de simples qubits sont capables de réaliser des multiplications de matrices de nombres complexes pratiquement instantanément...
Mais nous avons notre intelligence pas l'artificielle, hein ! La réflexion nous permet de trouver des raccourcis mathématiques et algorithmiques. Même s'il nous reste encore une marge de progression énorme.
Bits probabilistes
Et justement, notre intelligence nous a poussé à imiter la nature en transformant les problèmes en une recherche de minimum, et en introduisant une dose de bruit, d'aléa sur des nœuds ad-hoc.
Sauf que nous avons quand même les liens à gérer entre les nœuds, ce sont des calculs à réaliser classiquement. Et donc ces machines seront immanquablement limitées par le temps de calcul qui croitra avec le nombre de nœuds.
Tout ceci est très compliqué car vous avez compris que cela fait intervenir beaucoup de compétences disparates, non seulement les inévitables mathématiques, l'informatique mais aussi beaucoup de physique et de technologie dans des domaines divers et variés, qu'il faut être aussi plutôt bon en microélectronique pour sentir ce qui sera faisable lors de la mise à l'échelle.
J'espère que vous y voyez juste un petit peu plus clair à présent.