Les ordinateurs quantiques
Algorithmes quantiques
Explication par Shor himself, en 2 minutes:
Malheur. Enfin, pour vos méninges. Les miennes sont cramées depuis des lustres et ne risquent plus rien vous vous en rendez compte en lisant ces lignes.
Après avoir vu l'explication par son inventeur, et bien vous apprécierez peut-être la mienne. J'ai vraiment voulu comprendre.
L'invention date de 1994.
L'algorithme de Shor est une attaque purement mathématique (pas de side-channel ou de trucs de ce goût-là) permettant factoriser «facilement» un nombre. Or tout notre système de chiffrement actuel repose sur l'algorithme RSA, algorithme dont la clé est le produit de deux grands nombres premiers, et il est réputé très difficile de factoriser ce genre de nombre.
Algorithme mathématique
Si vous aimez les mathématiques, voici un article en français qui vous mettra sur la voie :
La cryptographie et les ordinateurs quantiques \ Ghazal Kachigar
https://cm2.ens.fr/content/la-cryptographie-et-les-ordinateurs-quantiques-g-kachigar
C'est une mathématicienne qui a écrit ça, et on voit bien que les aspects physiques la dépasse. Mais c'est du velu côté maths, j'en ai résumé les aspects les plus intéressants ci-après.
Les théorèmes et lemmes mathématiques sont décrits dans l'article, et débouchent sur une proposition qui n'est pas utilisable classiquement.
En effet, le résultat principal du théorème mathématique est que si on choisit un nombre « a » qui n'est pas un diviseur de notre clé « n » à factoriser évidemment, sinon on a trouvé, gros malin alors nous avons :
( ar/2 ± 1 mod n ) soit un diviseur de n
« a » est un nombre choisi au hasard !
Sauf que calculer la puissance d'un nombre modulo n, vu la taille des nombres (2048 bit pour RSA, c'est vraiment beaucoup), on ne risque pas d'y arriver avec un calculateur classique. Et le « r » qui est en puissance, on le trouve comment ?
Eh bien si a est co-premier avec n (aucun diviseur commun) alors :
La période r est aussi "l'ordre" de l'entier a modulo n, c'est-à-dire le plus petit entier pour lequel : ar= 1 mod n
Non seulement il faut calculer les puissances de « a », et en plus, on a un problème de recherche de période. Cela parait assez mal barré, départ arrêté…
L'algorithme est donc le suivant :
- Choisir a au hasard, avec a < n bien sûr
- Calculer le PGCD(a,n). S'il est différent de 1, on a trouvé un facteur de n. Terminé coup de bol monstrueux !
- Calculer la période r de la fonction at mod n : c'est là que l'ordinateur quantique intervient.
- Si r est impair, ou si ar/2 ± 1 mod n n'est pas un diviseur : caramba, raté, recommencer du début avec un autre a. On a mathématiquement prouvé que la probabilité était supérieure à 3/8, donc ça ne sera pas trop long.
- Calculer le PGCD(ar/2 ± 1 mod n , n) : le résultat est un diviseur non trivial de n (prouvé mathématiquement). Bingo !
Comment notre ordinateur quantique peut-il facilement calculer la période d'une fonction ?
C'est là que l'article mathématique se perd. Notre mathématicienne s'embarque alors dans une explication "intuitive" qui dit que grosso-modo, dans un ordinateur quantique à n bit, on a 2n états possibles et qu'on ne peut qu'en mesurer qu'un seul (ça, on avait compris). Mais que s'il existe une structure sous-jacente, alors elle devrait "ressortir". Alors là, comme explication, il va falloir mieux faire. Parce qu'elle s'arrête là !

Exemple de calcul
Un exemple ne fera pas de mal pour voir comment ça marche.
Trouver les facteurs premiers de n=314191
- On choisit 101 au hasard
- 101 et 314191 n'ont pas de diviseur commun : OK
- Trouver la période r de la fonction f(t) = 101t mod 314191
- On trouvera (plus loin) r = 4347 qui est impair: caramba, raté.
On recommence du début. - On choisit 127, toujours au hasard
- 127 et 314191 n'ont pas de diviseur commun : OK
- Trouver la période r de la fonction f(t) = 127t mod 314191
- On trouvera 17388. Ah, il n'est pas impair. C'est mieux.
- On ne calcule pas 12717388/2 mod 314191
on essaye directement:
PGCD(12717388/2 + 1, 314191) = 829 - PGCD(12717388/2 - 1, 314191) = 379
C'est mortel comme algorithme, quand même, non ?
Reste à voir comment trouver la période de la fonction
(oui, je sais il faudra recommencer avec 127).
Avec un hypothétique ordinateur quantique, maintenant qu'on sait comment rentrer une fonction :
- Il faut calculer les puissances successives de 101
et calculer le reste de la division par 314191
|x⟩ ⇒ |x,101x⟩ ⇒ |x,101x mod 314191⟩ - On va donc mettre en superposition tous les nombres entre 1 et (éventuellement) 314191
|1⟩ +|2⟩ +|3⟩ +|4⟩ +|5⟩ + … + |314191⟩
en réalité, on partira plutôt de |0⟩, mais c'est secondaire - Puis calculer la puissance de 101 puis le reste de la division par 314191 (le modulo, quoi)
- |1, 1011⟩ + |2, 1012⟩ + |3, 1013⟩ + … + |314191, 101314191⟩
- |1, 101 > + |2, 10201 > + |3, 1030301 > + … (puissance calculée)
- |1, +101 > + |2, +10201 > + |3, +87728 > + … (modulo calculé)
Si on lit cette fonction d'onde, on va obtenir un seul de ces résultats au hasard, suivant l'amplitude de chaque terme, a priori la même pour tous, et on sera bien avancé: ça ne nous donne pas la période, évidemment, juste un des calculs de puissance modulo 314191, par exemple |+74126⟩
Ce qu'on aimerait, c'est plutôt avoir les premiers termes de :
Dans tes rêves !
- Si on effectue vraiment le calcul à la main (et c'est pénible), on trouve :
|20⟩ + |4347⟩ + |8714⟩ + …La différence entre ces éléments donne p, ici 4347.
Manuellement, on le devine, mais comment faire dans un ordinateur quantique ? Ce qu'on veut, c'est uniquement la période, ou la fréquence 1/p.
Il faut faire une … transformée de Fourier quantique (ça existe, on dit QFT) pour trouver la fréquence.
- On passe donc à la moulinette de la QFT les termes :
|x⟩ + |x+p⟩ + |x+2p⟩ + |x+3p⟩ + … ce qui va donner :
|1/p⟩ + |2/p⟩ + |3/p⟩ … - On aura alors dans notre fonction d'onde, en superposition :
|1/4347⟩ + |2/4347⟩ + |3/4347⟩ …
soit |0.000235⟩ + |0.000470⟩ + |0.000706⟩ …
et comme d'habitude, quand on lit cette fonction d'onde, on ne lit qu'un seul résultat, avec une certaine probabilité, mais ce ne sera pas trop le problème ici. - Par exemple, on lit |0.001177⟩, et nous voilà bien avancés, car on ne sait pas lequel c'est. Alors on recommence ! On lit alors, au hasard, un autre terme, par exemple |0.001412⟩, puis une autre fois c'est |0.000470⟩. Au bout d'un moment, on finit par deviner la période: 4347.
- On vérifie le résultat en calculant (classiquement)
1014347
1014347 est peut-être un poil très gros comme nombre ? Il a vraiment déjà beaucoup de chiffres. Alors qu'on joue uniquement avec un nombre à factoriser de 6 chiffres, alors imaginez sur une bonne grosse clé RSA de 2048 bits, le nombre va être absolument gigantesque. Il va en falloir, des qubits !
Sauf que cet abruti de résultat 4347 est impair : ce n'est donc pas la bonne réponse vu qu'il faut le diviser par 2. Donc on recommence du début avec un autre nombre, par exemple 127.


Il nous faut donc apprendre à :
- Créer la suite 1,2,3… en superposition (ça, on sait faire avec Hadamard)
- Puis élever à la puissance d'un autre nombre et calculer le reste de la division par le nombre à factoriser (c'est la partie la plus dure en fait)
- Puis appliquer une transformée de Fourier quantique
En espérant que ce soit rapide à calculer, parce qu'avec un ordinateur classique, c'est catastrophique.
Algorithme quantique de Shor
Là, c'est vraiment l'enfer. La transformée de Fourier quantique QFT est inévitable -mais bon, on la voyait venir, non ? Et l'exponentiation modulaire, vous l'avez vu venir ?
Commençons par l'organisation générale, qui est plutôt simple sur le principe :
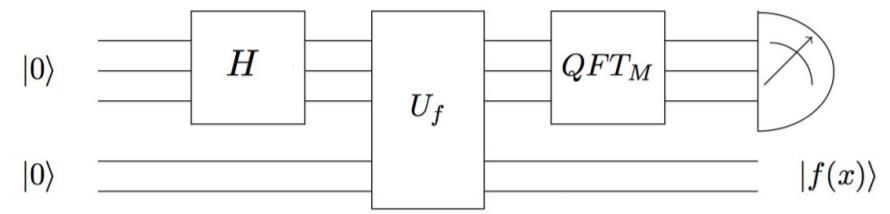
- Avec Hadamard, on commence par créer la superposition de toutes les valeurs du premier registre.
- Puis dans Uf, on calcule l'exponentiation modulaire, la fonction dont on veut trouver la période. Le résultat se situe dans le second registre, on doit faire comme ça, on a vu pourquoi lors de la création de fonctions. Créer cette fonction sera coton, car il faudra "coder en dur avec des portes quantiques" le nombre choisit au hasard et la clé à factoriser.
- Puis on applique la transformée de Fourier QFT, et on lit un résultat. On recommencera (probablement) plusieurs fois pour extraire la période, comme on l'a vu.
Transformée de Fourier quantique
Commençons avec la transformée de Fourier. Je ne vais pas faire un cours détaillé ici, vous trouverez ça sur le web, uniquement quelques intuitions.
Pour rappel, il s'agit de passer du domaine temporel au domaine fréquentiel (et réciproquement), et dans le quantique, cela revient "simplement" à changer de base. Pour changer de domaine, on va opérer des rotations : l'astuce consiste à se rappeler que les coefficients devant chaque élément de la base sont des nombres complexes, et que la partie imaginaire est une phase. Et là, vous devriez avoir l'intuition de ce qui se passe.
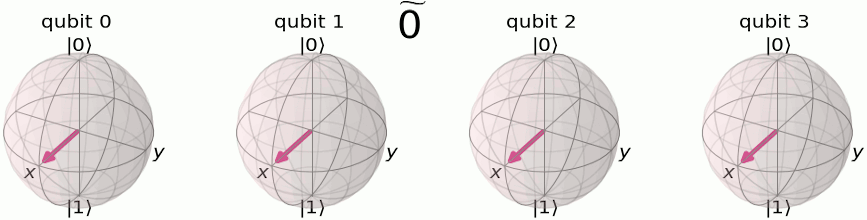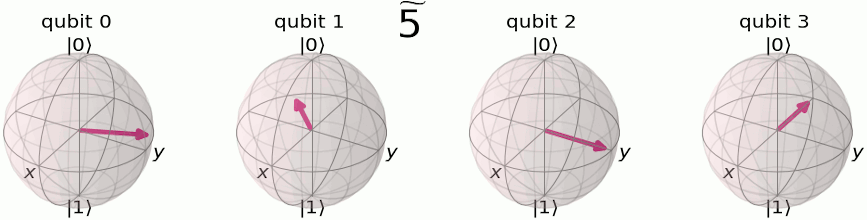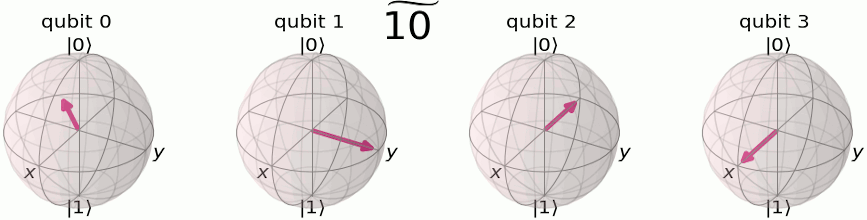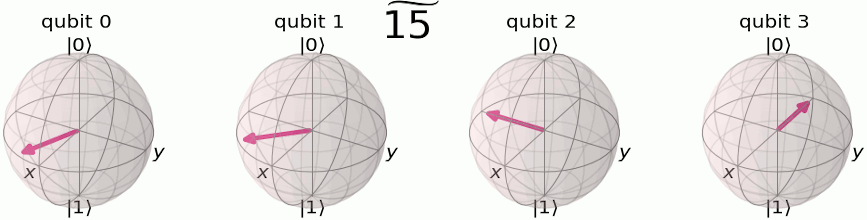
Par exemple avec 4 qubits :
Au début, nos qubits sont dans un état superposé, un état particulier étant le suivant dans la sphère de Poincaré :
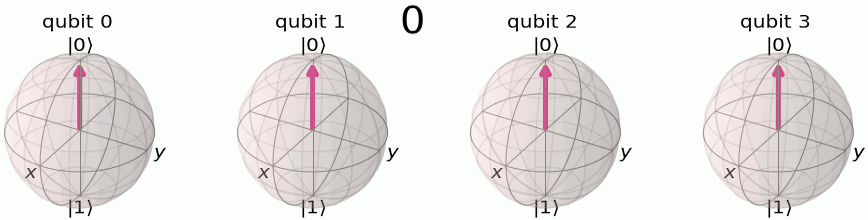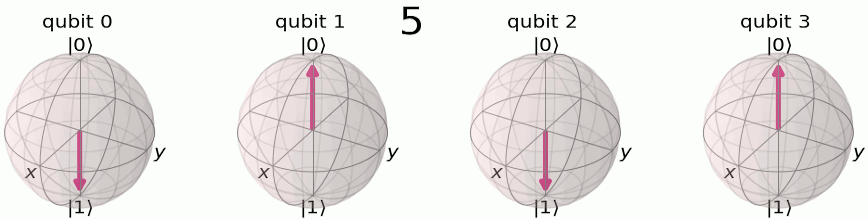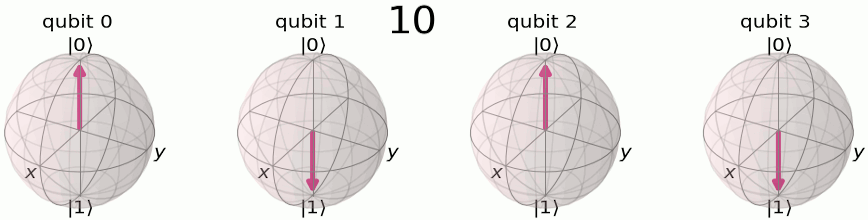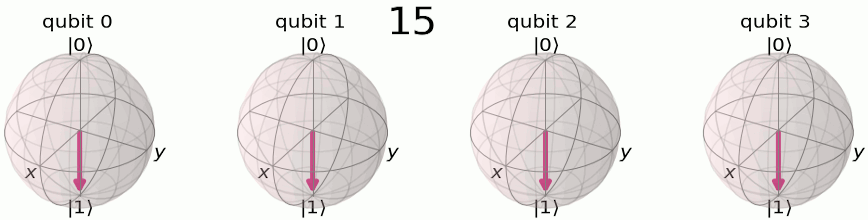
Eh bien on va faire passer notre état sur le plan milieu (donc obtenir un état équiprobable de |0> et de |1>, ce que fait Hadamard qui au passage réalise en fait une transformée de Fourier sur 1 bit et faire tourner notre vecteur, donc modifier sa phase —et ce sera périodique, c'est l'idée !— :
La transformée de Fourier quantique :
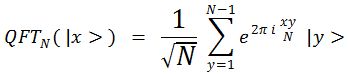
On voit donc qu'on aura besoin de faire tourner le vecteur, une fois qu'on l'aura mis "à plat" avec Hadamard. Donc une opération du genre :

Pour fixer les idées, voici à quoi ça ressemble pour 4 qubits :
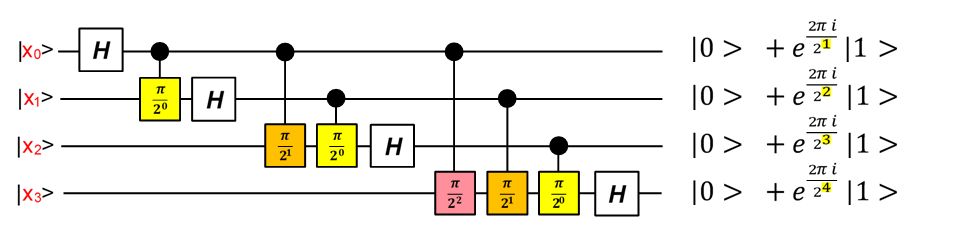
Nous avons n portes de Hadamard et n(n-1)/2 portes pour le contrôle des déphasages. En fait, ça ressemble beaucoup à la transformée de Fourier rapide si vous connaissez.
La transformée de Fourier quantique marche comme sa copine classique (elle est symétrique, pareil) :
- Si vous entrez un sinus pur et dur, alors en sortie vous obtenez un Dirac correspondant à la fréquence du sinus.
- Si vous entrez un Dirac, en sortie vous avez un sinus. Ce qui peut être commode pour générer des fonctions au passage. C'est d'ailleurs pour ça que l'opérateur Hadamard est en fait une transformée de Fourier sur un seul bit: on entre un Dirac (|0>) et il en sort un "sinus", moitié/moitié sur |0> et |1>.
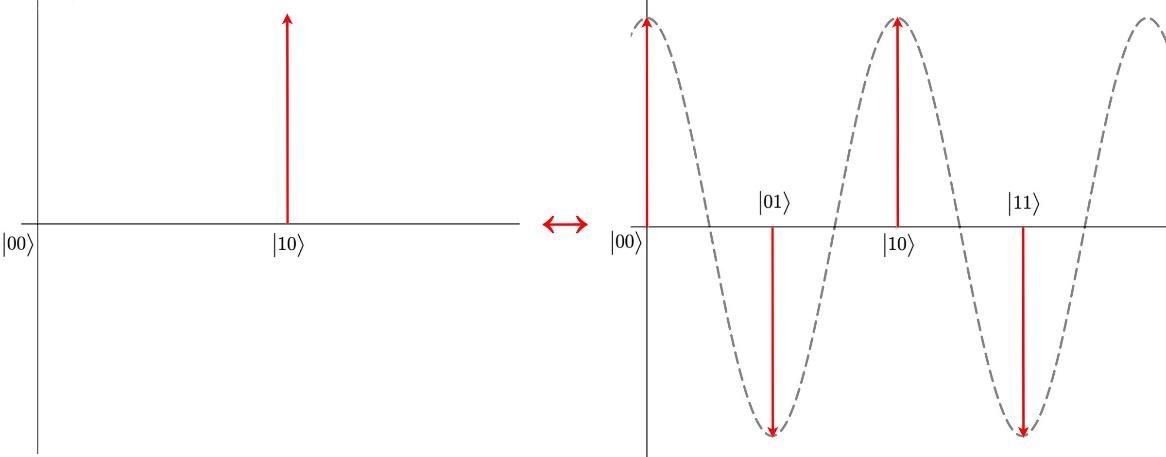
Exemple d'un Dirac en entrée sur 2 qubits.
Plus généralement, ça marche comme ça. Si on a en entrée un vecteur de dimension M (qu'on choisira souvent comme une puissance de 2 parce qu'on aime ça) présentant une période "r", alors le résultat aura des valeurs non nulles en M/r :

Ainsi, lorsque l'on va lire le résultat, on aura n'importe quel multiple de M/r, et donc il faudra exécuter plusieurs fois pour extraire la valeur r.
On remarque aussi que si la fonction d'entrée est décalée, ça se traduira par un décalage de phase = la partie imaginaire de notre vecteur. Le résultat sera inchangé à la lecture, ce qui est fort pratique.
En réalité, il va rester un peu de bruit, et pour extraire la valeur de la période, on a généralement intérêt à augmenter le nombre d'échantillons M.
Certes, mais pour notre problème, il en faudra combien ? Il existe au moins une proposition avec 2n+3 qubits pour un entier à factoriser de n bits. Avec 2048 bits, ça nous fait du 4000 qubits au bas mot (en supposant qu'il ne faille pas de correction d'erreurs !). Et des milliards de portes quantiques à appliquer. Il reste encore des progrès à faire pour casser du RSA.



Exponentiation modulaire
On a vu uniquement la partie "extraction de période". Il faut aussi "entrer" la formule de l'exponentiation modulaire pour calculer la fonction, et c'est là que le bât blesse en réalité.
Je ne vais pas entrer dans les détails ici pour réaliser cette opération.
Lisez l'article de Stéphane Beauregard :
Circuit for Shor's algorithm using 2n+3 qubits
Exponentiation modulaire
et là vous saisirez toute l'étendue du désastre :
la conception d'algorithme pour le quantique n'a rien à voir avec l'informatique habituelle, même si certains s'essayent à faire des parallèles.
Il faut définir des additionneurs modulo n, des soustractions (qu'on fait avec une addition encadrée par deux transformées de Fourier -bonjour la ruse-), du multiplieur, etc. Tout ça pour finir sur une usine à gaz, mais bon, il existe aussi des programmes informatiques bien tordus, et les concepteurs y sont pour quelque chose.
Un autre article, aussi complexe, mais plus pour matheux :
Shor's Algorithm for Quantum Factorization
http://tph.tuwien.ac.at/~oemer/doc/quprog/node18.html
Records de factorisation
On remarquera qu'on donne souvent 15 comme exemple de factorisation avec un ordinateur quantique réel. Remarquez que 15 est vraiment le tout premier nombre intéressant puisque ce sont les deux premiers nombres premiers après 2 (qui est trop facile à trouver). Et en plus, 15 requiert juste 4 bits, ça aide.
Ceci dit, c'est pratiquement un exercice d'école que de factoriser 15 avec l'algorithme de Shor.
Comme c'est un peu long à expliquer, autant aller voir directement l'explication avec Qiskit :
https://qiskit.org/textbook/ch-algorithms/shor.html
C'est bien expliqué pas à pas, vous avez tous les détails, avec les ruses, dedans.
L'algorithme de Shor n'est pas le seul proposé. Cet algorithme utilise un ordinateur quantique universel, mais d'autres solutions, en particulier basé sur le recuit simulé (annealing) sont proposés.
côté record, c'est actuellement le concours de celui qui aura la plus grosse. Factorisation, bien sûr. Et difficile de s'y retrouver dans tous les résultats.
À présent, on n'hésite pas à parler en "megaqubitdays", et là, ça fait peur. Schneier a repéré en 2019 un papier qui parle de factoriser RSA 2048 avec 20 millions de qubits.
2024
Un article difficile à lire pour non-initiés fait le point sur l'algorithme de Shor, et les conclusions sont pessimistes, comme d'habitude.
- 9th International Cryptology and Information Security Conference 2024 (CRYPTOLOGY2024)
- (page 48) Current Status on Shor’s Algorithm via Quantum Computing / Nur Azman Abu & Zahari Mahad
Pourtant IBM annonce pour 2025 un chip nommé Kookaburra avec 4158 qubits, donc ça augmente pas mal.
Et les chercheurs indiquent qu'ils ont besoin de 2m+6 qubits, m étant le nombre de bits de la clé RSA à factoriser (2048 bits pour rappel).
Mais avec des qubits qui marchent bien, sans trop d'erreurs...
Conclusion de l'article :
After 3 decades of its inception, Shor’s Algorithm is still crawling at its infant stage.
Vous en avez chié ? Moi aussi, si ça peut vous consoler.
Et sans trop me jeter de fleurs, j'estime que mon explication est certainement la plus facile d'accès.
En conclusion, je vous le dis, mes bien chers frères, cette histoire de factorisation semble plutôt faisable, mais il va falloir un ordinateur quantique de malade, plein de qubits, pour craquer RSA. Mais celui qui le fera aura le Nobel. Sauf qu'il n'aura pas le droit de dire qu'il a réussi, l'État se chargera de lui.
La prochaine page est une tentative d'essai d'utiliser un vrai ordinateur quantique, histoire de voir si j'en étais capable.