Les ordinateurs quantiques
Algorithmes quantiques
Attention : c'est là que ça se joue.
On va appliquer la fonction qu'on veut, avec tous les calculs superposés simultanés, alors que normalement ça n'aime pas ça.
Pour rappel, les opérateurs DOIVENT être unitaires et inversibles (ou réversibles) : pas question d'appliquer une fonction qui irait "que dans un sens" et qui aurait un nombre de qubits différent entre l'entrée et la sortie.
Mais on ruse: on ajoute des qubits "qui ne servent pas", et on peut construire une matrice telle que la sortie soit un XOR (= addition modulo 2) sur une partie des qubits :
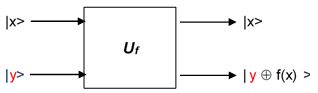
Comment on peut réaliser cela physiquement ? Pour l'instant, on met ça de côté comme dans tous les articles sur ce sujet, on verra ça dans les machines quantiques.
Évidemment, appliquer la matrice sur un vecteur d'entrée, ça se fait "d'un coup" et c'est parallèle. Sauf qu'en sortie, on n'aura pas le résultat, juste une probabilité d'apparition de "quelque chose". Il va falloir ruser pour sortir un algorithme utilisable, et d'ailleurs il n'en existe pas des tonnes (pour l'instant).
On déduit facilement du cas général une implémentation assez simple : on garde n qubit sur |x>, et on prend un seul qubit pour |y> qu'on colle à zéro, comme ça le XOR est trivial une addition avec zéro, c'est à ma portée. On colle du Hadamard pour générer tous nos états superposés, et voilà ce que ça donne :
Imaginons que nous ayons une fonction f souvent appelée "oracle", allez savoir pourquoi qui donne un résultat qui est zéro ou un, dépendant de la valeur des qubits d'entrée. Comment est la matrice ? Nous allons détailler ce que ça donne pour le cas d'une fonction sur un seul bit d'entrée -et ça permettra de réviser.
Exemple avec une fonction à un bit
Avec 1 seul bit d'entrée, il n'y a pas cinquante mille fonctions possibles, mais uniquement 4 (1 bit à 2 états en entrée, 1 bit à 2 états en sortie soit 2x2).
Choisissons une des quatre fonctions, par exemple f3, celle qui sort toujours 1. En entrée, un seul qubit pour |x⟩ (c'est une fonction avec 1 seul bit), on ajoute un qubit pour la seconde entrée |y⟩, et en sortie nous avons forcément 2 qubits. La matrice correspondante est la suivante (calculée par ailleurs), et rappelons la définition des vecteurs on se ramasse facilement sur l'ordre:
En pratique, le second qubit |y⟩ sera souvent |0⟩.
Voici le résultat suivant les 2 vecteurs d'entrée possibles, ce qui permet de vérifier que la matrice effectue bien f3(x):
Le résultat indique que si on mesure la sortie, avec l'entrée donnée, alors on lira à coup sûr le résultat "1" avec une probabilité de 100% sur le second qubit. Il s'agit bien de f3.
Le cas général est:
On a donc intérêt à mettre sur l'entrée |x> une superposition d'état, par exemple avec Hadamard qu'on a vu juste avant, et |0> sur la seconde entrée.
On voit que la fonction exécute les deux évaluations, pour |0> et |1> en même temps, les deux résultats sont superposés dans la sortie. Si on effectue une mesure, alors on aura à égalité de chance :
- Mesure : |01> (c'est le vecteur 0,1,0,0) soit f(0)=1 : on a à la fois le "x" (premier qubit) et le résultat de la fonction dans le second qubit.
- Mesure : |11> (c'est le vecteur 0,0,0,1) soit f(1)=1
Il faut faire deux mesures au minimum (en ayant de la chance) pour connaitre le résultat de la fonction. Ce qui est évidemment d'un intérêt relatif puisqu'en classique, on exécute la fonction 2 fois et c'est fini.
Et en plus, il aura fallu entrer la bonne matrice -donc la bonne fonction- à appliquer dans le système, ce qui signifie qu'on connaissait déjà la fonction (normalement !).
Avec un nombre de qubits en entrée plus important, cela parait plus intéressant. En effet, avec n qubits pour les |x> où on superpose tous les entiers entre 0 et 2ⁿ-1 (avec Hadamard), on va calculer la fonction f(x) pour toutes les valeurs en une seule passe, au lieu de 2ⁿ en classique. La puissance de l'ordinateur quantique réside là : les calculs simultanés en parallèle/superposés.
Un vrai additionneur
Voici un exemple concret, calculé avec un véritable ordinateur quantique garanti d'origine.
On veut réaliser toutes les additions possibles avec 3 bits d'entrée, le résultat se trouvant sur 2 bits :
On entre le programme dans le logiciel d'IBM, puis on l'exécute :
Le programme est assez simple: le premier bit résultat est la somme des bits modulo 2, on voit bien qu'on prend chaque bit d'entrée une seule fois successivement.
Le second bit, c'est la retenue, on prend toutes les combinaisons des bits d'entrée deux par deux pour les additionner, modulo 2.
Ensuite, on lit le résultat. Je n'ai pas fait le malin !
IBM a le bon goût de nous simuler la fonction, et de nous donner les résultats dans la fenêtre en bas à droite "probabilities". Comme c'est une simulation, la prédiction est parfaite : les 5 bits lus contiennent les 3 bits d'entrées, puis les deux bits résultants de l'addition. Youpi.
En bas à gauche "result-histogram", vous voyez le résultat réel d'exécution : et bien les bonnes réponses sortent du lot.
Du coup, on est sur notre faim : OK, on peut faire beaucoup de calculs en parallèle. Mais on ne peut pas extraire facilement le résultat ! Il va donc falloir trouver mieux pour exploiter ça. Et ce ne sont pas les raisonnements algorithmiques classiques qui vont nous aider, ça n'a absolument rien à voir.