DCF 77
Les signaux issus des modules de réception sont loin d'être parfaits, ils peuvent facilement contenir des parasites, aussi il est souvent très utile d'effectuer un filtrage.
Et là, de nombreuses propositions existent, parfois douteuses, parfois excellentes.
Exposé du problème
Pour ceux qui n'ont pas bien suivi, nous avons un module DCF77 qui ressemble à ça :

Et qui devrait sortir ça :
Ce genre de module va très bien marcher non loin de l'émetteur de Mainflingen car le signal sera fort et assez constant. Mais sans pour autant être exempt d'ennuis liés aux parasites environnants, et autres problèmes liés au soleil.
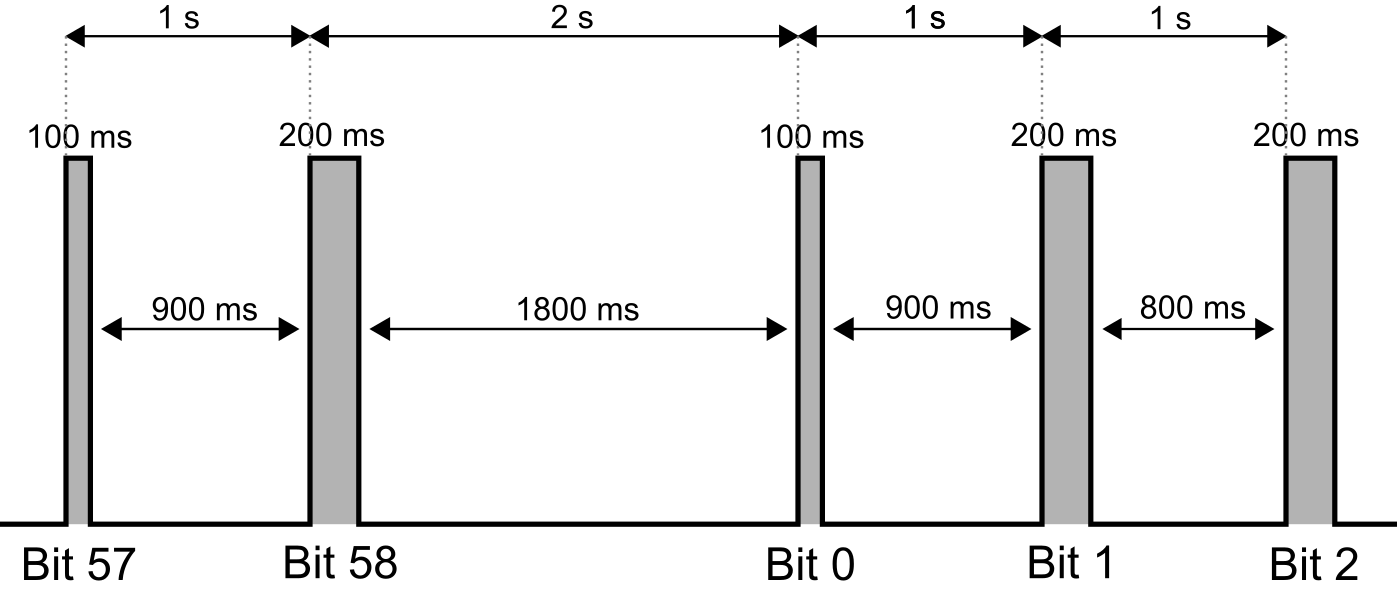
Ce que l'on souhaite, c'est un signal propre "comme dans la doc", pas forcément super-bien calibré en largeur mais suffisamment pour distinguer un créneau de 100 m d'un créneau de 200 ms, et surtout sans "glitch", sans impulsion supplémentaire, car ce qu'on aime bien faire avec un microcontrôleur ou un programme, c'est asservir sur un "front montant" puis un "front descendant". Alors forcément, si on a des fronts supplémentaires, ça devient vite pénible...
Notez que le signal est "négatif", il est à zéro sauf lorsque la
modulation diminue où la sortie passe à 1, sans valeur intermédiaire.
Accessoirement, c'est le plus simple à saisir, ça tombe bien.
Idéalement, comme on connait la forme du signal à recevoir, il vaudrait mieux faire un filtre qui soit exactement adapté à ce signal, il serait alors infiniment meilleur que n'importe quel autre filtre.
Les propositions du Net
Les sites suivants contiennent des infos parfois intéressantes concernant la réception et le filtrage :
- Dans CHOUR - Horloge DCF77 sur processeur MSP430, un échantillonnage est proposé pour détecter le début de trame, mais il faut que le signal soit déjà "assez propre".
- DCF77 Radio Clock de SinelaboreRT, qui manifestement doit recevoir un signal fort et clair, ça aide.
- [2018] DCF77 Based Long-Term Timer est une étude de Jianwei Sun / ETH en Suisse. Contient une comparaison de quelques récepteurs DCF77, mais bon, manifestement il reçoit un bon signal, ça se voit dans ses statistiques de réception, alors il peut faire simple, il attend gentiment d'avoir une trame complète pour se synchroniser, c'est d'un intérêt relatif (il vit dans un monde de Bisounours, il ignore les créneaux suivants une détection pendant 980 ms). Montre les effets néfastes des écrans LCD et des alims à découpage, mais ce n'est que qualitatif.
- Performance Analysis and Receiver Architectures of DCF77 Radio-Controlled Clocks / Daniel Engeler. Propose un algorithme sur FPGA (basé sur une transformée de Fourier couplé à un détecteur particulier), et compare avec la solution de démodulation basique à diode. Toutes sortes de bruit sont ajoutés pour voir les effets et montrer les performances obtenues.
- Yet another Radio Clock propose un filtrage sur un Cortex d'ST.
- [2018] Data Extraction from the Distorted DCF77 Signal Captured Using Low-Cost Receivers il faut payer pour connaitre le contenu
- [2013] Software Defined DCF77 Receiver / Filip ZÁPLATA, Miroslav KASAL. Le signal RF est directement converti par un ADC, puis décodé.
- [2012] Blinkenlight (Udo Klein) s'est vraiment attaqué au problème du filtre, et propose le "filtrage exponentiel". Il explique comment filtrer, comment ça marche pour ce cas particulier. Avec cela, on peut extraire un signal avec plus 80% de bruit, ce qui est impressionnant. Mais il ne s'arrête pas là et explique aussi comment aller plus loin en sortant l'artillerie lourde de la boucle à verrouillage de phase, en détectant la phase par un calcul de convolution.
- astoeckel / libdcf77 (github) propose un filtre passe-bas (numérique) associé à un trigger de Schmitt, c'est plus ou moins le premier pas du précédent.
- ...
Pour faire court, c'est Udo Klein qui décrit ce qui est probablement la solution la plus simple et la plus efficace. Je vais vous en faire un résumé, ce qui me sera utile au passage pour porter ce filtre sur MSP430, pour ma propre horloge DCF77.
Passons aussi sur les horloges DCF77, certaines très intéressantes au demeurant vues que c'est le genre d'horloges que je souhaite réaliser ─mais avec un anneau de 60 neopixels et un MSP430, mais qui :
- soit réutilisent le superfiltre d'Udo Klein
- soit reçoivent un signal DCF tellement propre qu'il n'y a rien à faire
- ou rien n'est vraiment intéressant dans le code
- DCF77 Radio Clock de SinelaboreRT, qui manifestement doit recevoir un signal fort et clair, ça aide.
- Performance Analysis and Receiver Architectures of DCF77 Radio-Controlled Clocks / Daniel Engeler. Propose un algorithme sur FPGA (basé sur une transformée de Fourier couplé à un détecteur particulier), et compare avec la solution de démodulation basique à diode. Toutes sortes de bruit sont ajoutés pour voir les effets et montrer les performances obtenues.
- [2012] ondrejh / msp430_dcf77_clock du code pour MSP430. Effectue un échantillonage toutes les millisecondes, mais bon, il reçoit certainement un bon signal car le décodage est assez simple, fait des statistiques sur le 100 premières ms puis les 100 suivantes, ça marchera avec des signaux assez propres. Pas de vrai filtrage.
- [2013] Réveil "Lever de Soleil" / Renaud Schleck. Egalement sur MSP430. Utilise des interruptions sur les signaux en provenance du module DCF77, il faut un signal propre pour que ça marche. Pas de filtre. Il doit habiter près de l'Allemagne...
- Arduino DCF77 Analyzer Clock MK2.
- Arduino DCF77 Signal Analyzer Clock Utilise le "superfilter" sur Arduino d'Udo Klein.
- ...
Les liens ci-dessus pourront éventuellement vous donner des idées.
Le filtrage exponentiel d'Udo Klein
Avec un nom pareil, j'ai l'impression d'entrer dans l'Excelsior de Star Trek... Ah ben non, c'était de l'hyperexponentiel, rien à voir.
Vous pouvez regarder avantageusement la description originale d'Udo Klein. Je ne fais que transposer sa proposition.
Certes avec quelques commentaires de mon cru, et à ma façon.
On s'arrange pour faire des calculs sur des entiers, pour ne pas consommer trop de CPU. Le signal d'entrée est échantillonné toutes les millisecondes, avec des valeurs qui sont soit 0 soit 10000, pour des calculs sur 16 bits.
Pour chaque échantillon x(t), on va calculer une valeur smoothed w(t) :
On s'arrange pour que le signal smoothed w(t) soit affaibli à 50% de sa valeur après au plus 50 ms, qui est la moitié de 100 ms, la largeur du signal pour zéro, qui vaut 200 ms pour "un", (imaginez que l'entrée x(t) soit nulle).
Pour cela, il faut fixer la valeur N à 72.635, qu'on arrondit à 72.
Pour quel effet ?
- Avec un et un seul échantillon à 10000 pour x(t), autrement dit un pic unique (un Dirac) avec un signal à zéro, alors on aurait un petit pic de 10000/72 = 139, qui s'affadira doucement (car on garde quasiment la valeur précédente (N-1)/N).
- A partir de zéro, un signal constamment à 10000 provoquera une montée relativement lente de w(t), pour atteindre 5000 après 50 pas.
- En résumé, toutes les petites imperfections sont extrêmement atténuées car le signal entrant compte pour une petite part.
On peut calculer plus facilement w(t) avec :
Ce qui est d'un intérêt relatif car α = 1/N qui est plus petit que 1, or on veut des calculs entiers...
Sauf que l'on voit que la variation entre deux échantillons consécutifs w(t)-w(t-1) est proportionelle à la différence entre l'entrée et l'échantillon précédent. C'est là qu'on a un amortissement exponentiel de la valeur, d'où le terme.
Pour retourner un signal carré, il suffit de mettre un seuil sur le signal smoothed, ici ce sera 50% soit 5000 pour fixer la valeur de la sortie.
Sauf qu'une telle manœuvre est très risquée, car il suffirait que le signal oscille un peu autour de 50% pour provoquer des oscillations néfastes. Alors, à chaque changement de niveau (quand la sortie était à 0 et que le signal passe au-dessus de 5000, ou quand elle était à 1 et que signal passe en dessous de 5000) le signal smoothed est également altéré : il passe à 0 ou à 10000, suivant le cas. Du coup, il ne pourra pas changer avant 50 nouvelles valeurs au maximum en entrée. C'est l'hystérésis annoncée.
Le site d'Udo Klein donne un exemple d'exécution :
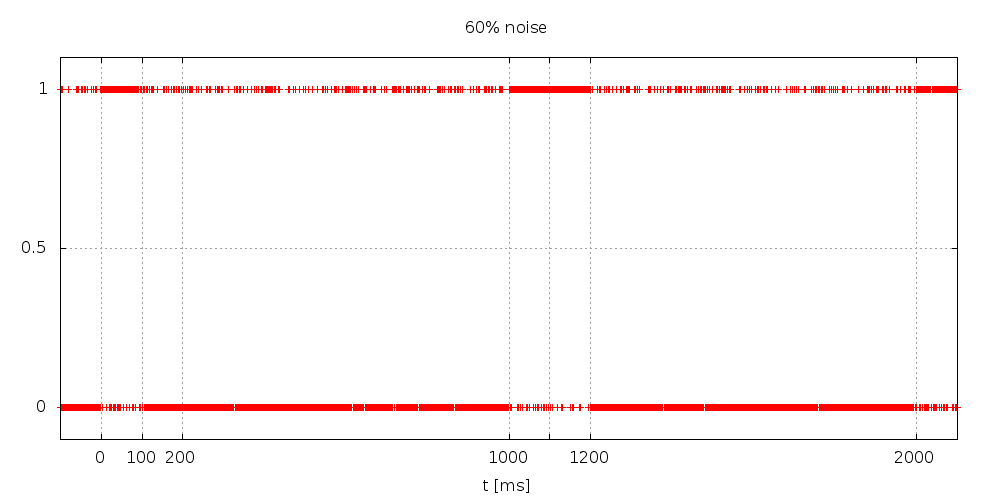
NOTEZ que ce bruit est un peu spécial : c'est de la "grenaille", plein de petits pics.
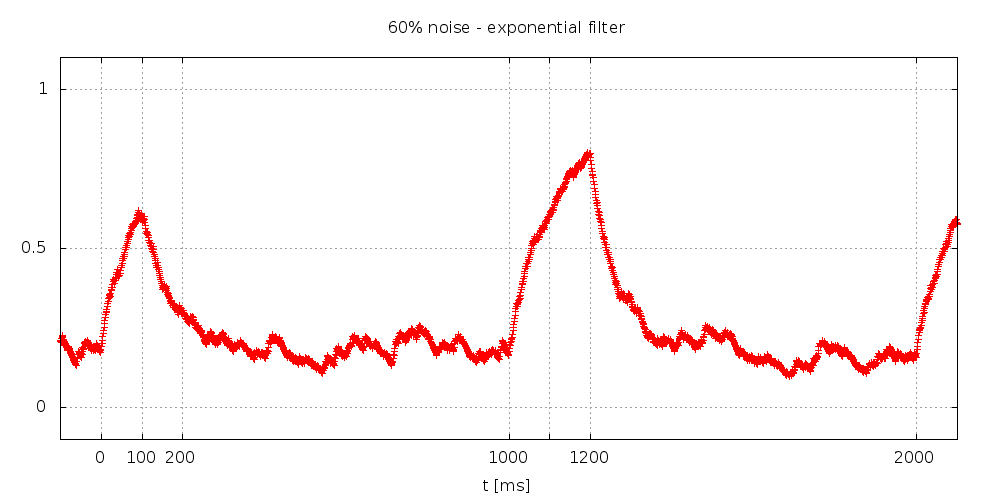
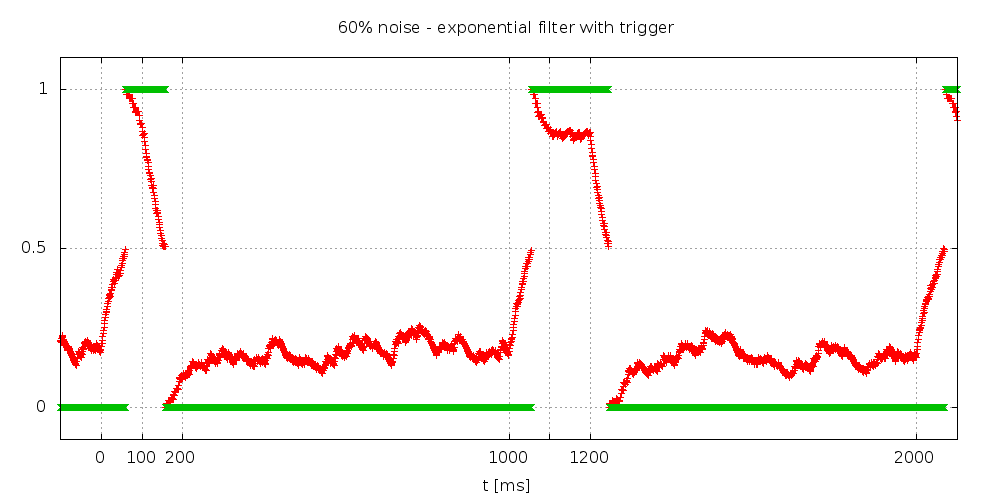
L'efficacité est remarquable !
Notez que comme tout filtre qui se respecte, un retard est introduit, forcément.
Optimisation de la vitesse d'exécution
Idéalement, il ne faudrait ni division, ni multiplication.
Les divisions
Les divisions sont extrêmement coûteuses en temps lors de l'exécution du programme sur des microcontrôleurs, il faut les éviter au maximum. Dans le programme d'Udo Klein, il existe une division par 72, qui est évitable en choisissant judicieusement les paramètres.
Par exemple, il vaut mieux diviser par 64 qui est un simple décalage à droite de 6 bits. C'est faisable si on modifie la vitesse d'échantillonage de 1000 μs (soit une milliseconde, valeur souvent choisie) à 1136 μs. Ce qui est facilement réglable dans un microcontrôleur grâce aux timers.
Les multiplications
Si le microcontrôleur ne possède pas de multiplieur interne dédié, alors il vaut mieux éviter les multiplications. Ici nous avons une multiplication par 71, ce qui n'est pas commode.
Comme nous avons modifié la valeur de N, qui passe de 72 à 64, N-1 devient 63, nous sommes en face d'une multiplication par 63. Ce qui peut devenir une multiplication par 64, qui est un simple décalage à gauche de 6 bits, suivi d'une soustraction de la valeur initiale.
On peut éviter toutes les multiplications et divisions, et avoir un code très efficace, en choisissant judicieusement les paramètres.
Tests effectifs
J'ai testé ce filtre passe-bas exponentiel avec un module DCF et un microcontrôleur MSP430.
Mon principal problème est la réception du signal DCF77. Entre les montagnes, je sais que je reçois modérément du signal, qui est très variable, je dois être souvent dans le cas où la réflexion sur l'ionosphère provoque des interférences, destructives et constructives, en voici la preuve.
J'ai implémenté le filtre passe-bas exponentiel avec un échantillonage au pas de 1136 μs, ce qui permet de réaliser des multiplications/divisions uniquement avec des décalages et additions. Il suffit de sortir le signal filtré sur une sortie du MSP pour observer le résultat.
Bonne réception
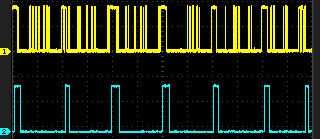
On voit ici que c'est vraiment très utile ! Pas évident de retrouver ses petits...
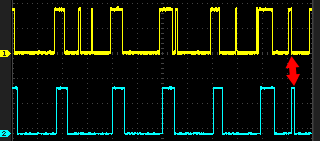
Notez le (petit) décalage temporel lié à l'exécution du filtre.
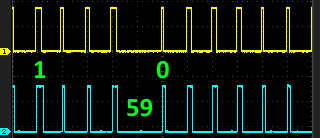
Au passage, on voit le "trou" de la seconde 59, suivi du "0" de 100 ms
Le "1" de 200 ms correspond au "2" des dizaines de 2024 (bit 55).
Mais pas toujours
Mais le signal peut subitement se dégrader sans raison apparente.
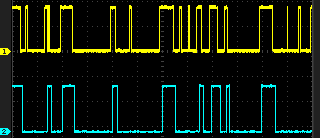
Mais on sent que c'est récupérable en filtrant mieux.
C'est là que l'on voit les limites du filtre passe-bas exponentiel. Udo Klein a réalisé des simulations avec beaucoup de bruit, mais pas du bruit de ce genre, avec des gros créneaux. Je pense que mon module de réception réalise déjà du filtrage et élimine tous les petits glitchs comme ceux ajoutés dans les simulations.
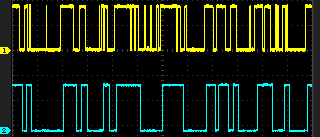
Ignorer le signal pendant 800 ms
Une fois que l'on a trouvé au moins un créneau valide de 100 ou 200 ms, si on est sûr de son coup, alors on peut purement et simplement ignorer le signal provenant du module pendant 800 ms car on doit avoir zéro.
Pour faire ça, lorsque le signal filtré monte à 1 en début de seconde :
- on déclenche un timer de 900 ms (environ)
- dès que le signal filtré est redescendu à 0 (et pas avant !), on force la valeur à 0 (on ignore le module)
- quand le timer indique que les 900 ms sont écoulées, on reprend l'écoute pour détecter le prochain front montant (filtré)
A la seconde 59, il n'y a aucun front, l'attente sera plus longue d'une seconde.
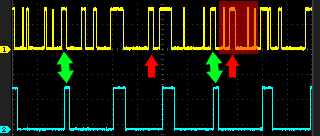
C'est violemment filtré, mais efficace... Des gros créneaux sont éliminés.
De cette manière, on nettoie encore plus efficacement le signal. Mais il faut avoir confiance dans la détection du début de seconde (pas si évident), et aussi dans son horloge locale (mais là c'est plus facile, on ne demande pas la Lune).
Ceci dit, si on n'a pas de chance et que nous n'étions pas calé sur le début d'une vraie seconde, comme on attend le créneau suivant, on a toutes les chances d'arriver sur un bon créneau, sauf à avoir vraiment beaucoup de bruit. On a alors réalisé un début de boucle à verrouillage de phase... sans s'en rendre compte !
En conclusion partielle, cette histoire de filtre passe-bas exponentiel peut être commode pour réaliser un petit module intermédiaire entre le module de réception DCF et une pendule, éventuellement en formatant les signaux à 100 et 200 ms, à condition de ne pas être trop regardant sur le calage temporel des signaux.
Mais en pratique, la détection de phase offrira de meilleures performances, nous abordons cela dans la page suivante.