Radiomètre de Crookes
Typiquement, avec autant d'hypothèses ou d'explications plus ou moins plausibles, il est important d'expérimenter avec des conditions variables afin de démêler la situation.
D'autres expériences, parfois assez habiles et subtiles, vont nous aider. Mais ce n'est plus au niveau du scientifique amateur, car il faut du matériel ad-hoc, faire du vide n'est pas à la portée de tous.
Quelles sont les variables ?
Il faut se poser la question des variables qui paraissent importantes. Personnellement, voici celles que je vois à l'issue des essais précédents, mais aussi ce que la logique me conseille (en clair, c'est le bon moment pour faire un brainstorming) :
- La pression, nous l'avons déjà vue, une courbe en forme de cloche.
- Utiliser différents types de gaz. La taille et les caractéristiques des molécules est probablement un paramètre de second ordre, mais il faut le vérifier, on aura peut-être des surprises.
- L'intensité des radiations : il semble bien que la force soit linéaire de l'énergie envoyée sur les pales. Mais bon, si on pouvait mesurer la température de chaque côté de la pale de préférence sans la perturber, ce serait bien mieux. Voire imposer la température, mais on sent que ça ne sera pas simple sur un truc qui tourne.
- Changer les caractéristiques thermiques des pales. Par exemple, isoler thermiquement les deux côtés de la pale. Ou changer leur nature.
- La forme des pales, et là nous avons plusieurs sous-variables :
- La surface de la pale.
- L'épaisseur de la pale.
- le ratio de la surface par rapport au périmètre. Un disque aura le périmètre le plus faible.
- Faire "beaucoup de trous" pour avoir beaucoup de bords.
- Comment séparer un effet "de bord" avec les autres effets ?
- La distance entre les pales et le verre est probablement un paramètre secondaire, mais il faudra le vérifier.
Étude statique
Afin de mesurer et comparer les forces appliquées, une seule pale sera utilisée, montée sur un axe fixe où on pourra mesurer une force avec une précision de l'ordre du dixième de microNewton. Et cerise sur le gâteau, en ajoutant une résistance chauffante, on va pouvoir maitriser les températures. Ceci dit, la pale n'étant pas en mouvement, ce n'est pas exactement la configuration du radiomètre, mais au moins, on élimine encore un autre paramètre (la rotation). Il existe d'ailleurs des discussions à ce propos.
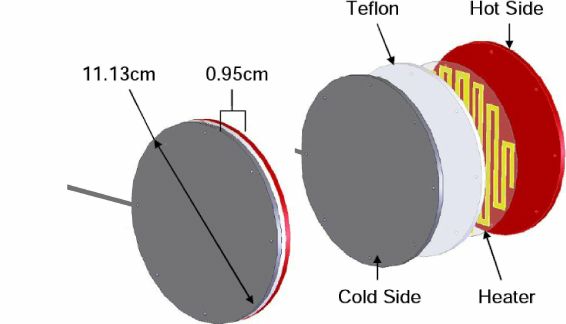
Avec ce genre de dispositif, on peut appliquer une différence de température de l'ordre de quelques dizaines de degrés, ce qui permet d'analyser systématiquement diverses configurations, puis de confronter avec des simulations.
Voici quelques exemples de résultats pour illustrer ça :
On remarquera l'extraordinaire linéarité du phénomène.
Rapport entre la surface, le périmètre : ceci permet de commencer à différencier les effets de bord, et les effets liés à la surface.
Comme il existe une tirée de paramètres, beaucoup de résultats ont été produits, ce qui a permis de commencer à dépatouiller toute cette histoire. Je ne détailleraí pas tout ici, ce serait vraiment très long et d'un intérêt relatif, le principal étant de savoir que l'on a pu faire des acquisitions précises.
Et on se rend compte que le type de gaz est important, donc les histoires de libre parcours moyen doivent être importantes. La taille du radiomètre aussi, mais bon, c'est secondaire.
Un peu de biblio pour ceux qui veulent creuser (une sélection de ma part, il y en a d'autres) :
- [2007] Experimental and Computational Observation of Radiometric Forces on a Plate / N. Selden, C. Ngalande, and S. Gimelshein
- [2009] Experimental and Numerical Analysis of Radiometric Forces on a Heated Circular Vane in Argon / Selden, N. Ngalande, C. Gimelshein, N. Gimelshein, S. Ketsdever, A.
- [2011] Analysis and Applications of Radiometric Forces in Rarefied Gas Flows / Sergey F. Gimelshein et als.
Radiomètre horizontal
Les chercheurs sont souvent astucieux pour contourner des problèmes de mesure, et séparer les effets. En voici un joli exemple : le radiomètre horizontal, aussi appelé radiomètre de Hettner car ce dernier avait fait, en 1924, des mesures uniquement sur le gradient de température avec un montage ad-hoc (mais pas forcément pour expliquer les histoires du radiomètre de Crookes).
La simple vue du dispositif ci-dessous devrait vous faire réagir
😮
(ah oui, pas mal, et ça marche ?) :

Alors évidemment, comme il est à plat, plus question de différence de pression et de force d'Einstein ! Il ne doit rester que les histoires de transpiration. Sauf qu'il doit exister une différence de température, donc de pression, entre le côté blanc et le côté noir, donc "du vent", mais bon, il n'est pas forcément juste le long des pales...

Le dispositif tourne "le blanc (froid) en avant". Ouf, ça correspond bien à la transpiration thermique, c'est la force de réaction par rapport aux molécules qui vont dans l'autre sens.
Radiomètre concave
Pas besoin d'avoir une face claire et une face sombre: une pale dissymétrique, présentant une concavité, aura une élévation de température plus importante d'un côté que de l'autre.
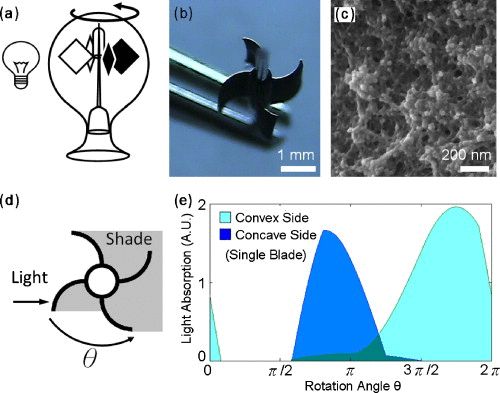
(b) the created light mill at the tips of tweezers;
(c) SEM image of closely packed gold nanoparticles on the porous light mill blade;
(d) illustration of asymmetric irradiation on the light mill, which rotates in the indicated direction;
(e) simulated rates of light absorption by the convex and concave surfaces at each blade vs the light mill rotation angle; integrating the areas below each curve shows an approximately doubled rate of heating at the convex side compared to the concave side.
Light-powered micromotor driven by geometry-assisted, asymmetric photon-heating and subsequent gas convection
La partie convexe chauffe plus que la partie concave, un gradient de température se forme, et la partie convexe est "poussée" (à l'inverse d'un "vent solaire", c'est contre-intuitif).
Nous voici donc à la tête de pas mal de résultats de mesures, reproductibles à souhait. C'est la base pour vérifier si les théories avancées se vérifient ou non...