Intro à la mécanique quantique
Cette histoire d'intrication a vraiment fait couler beaucoup d'encre.
En effet, on a l'impression de violer un poil la théorie de la relativité : avec une communication instantanée, plus rapide que la lumière ! Ou alors il existe une variable cachée que les photons partagent.
Les chercheurs ont alors essayé de faire la part des choses. C'est là qu'un dénommé Bell a exhibé une inégalité que l'on pourrait tester pour en avoir le cœur net.
En fait, on s'est rendu qu'on devait violer au moins une de ces trois règles :
- Causalité relativiste : on viole la vitesse de la lumière en envoyant un signal
- Variable cachée locale : la mécanique quantique est incomplète et ne décrit pas entièrement la réalité
- Principe de localité : deux particules éloignées forment deux entités pouvant être considérées indépendamment l'une de l'autre, chacune étant localisée dans l'espace-temps
Pas de transmission d'information
plus rapide que la lumière
Ouf ! Je ne veux pas d'ennuis avec la police de la relativité
Mais attention, c'est plus subtil qu'il n'y parait. Avec un tel système, on ne transmet pas d'information plus vite que la vitesse de la lumière : c'est juste que le premier détecté "prévient" le second de l'état à prendre.
En effet, quand on mesure l'état côté A, on n'est guère plus malin qu'avant car c'est un état aléatoire. Certes, on connait à présent l'état de A, et on sait que B aura le même, mais impossible pour B de savoir si cela contient une information : la position est aléatoire pour lui aussi, vu de sa fenêtre.
Les deux ne pourront vérifier que c'est bien la même polarisation qu'en échangeant cette information sur un canal de communication classique, lent.
Tout ce qu'on a, ce sont deux suites de nombres aléatoires en A et en B, qui sont corrélées. Et rien de plus.
C'est comme si on jetait une paire de dés, et qu'on obtiendrait TOUJOURS des paires. Un dé est envoyé sur Proxima Centauri c'est assez loin, effectivement, mais pas tant et l'autre reste sur Terre. Et si on tire d'abord un cinq sur Terre, alors le dé "frère" fera toujours un cinq sur Proxima Centauri, même lancé un siècle plus tard.



C'est du délire, je vous le dis depuis le début. Mais c'est la réalité.
Mais alors, qui on viole ?
Évidemment, on a voulu savoir quelle hypothèse est violée. A votre avis, c'est laquelle ?
- Transmettre une info plus vite que la vitesse de la lumière ? C'est méchamment suspect.
- Il existerait une variable locale cachée ? Du jamais vu. Comment ça marche ?
- Les deux photons ne respectent pas le principe de localité ? Dur à avaler quand même.
- 1, 2, et 3 à la fois donc réponse 4 ?
C'est là qu'un dénommé Bell a sorti le grand jeu mathématique, car si on respecte certaines hypothèses, alors cela a certaines conséquences. Ce sont les fameuses inégalités de Bell, et son théorème.
Il existe une histoire d'angle
La même expérience avec un bien plus joli dessin et des signes cabalistiques :
Il faut se souvenir ici que c'est en 3D, et non à plat. Les cubes séparateurs A et B peuvent tourner, et avoir un angle entre eux, angle qui vaut a côté A et b côté B par rapport à une référence commune. Dans ce qu'on a vu précédemment, on les a supposés alignés, avec b-a=0.
Si jamais on fait un angle relatif (b-a) non nul entre les deux cubes séparateurs, alors les polarisations ne sont plus alignées, forcément. On observe en fait une probabilité de coïncidence qui vaut :
Et évidemment le sin² pour les deux autres, P+- = P-+ , que je résume ci-dessous pour quelques valeurs d'angles remarquables :
La probabilité revient évidemment à compter les coïncidences pendant une durée assez longue pour que ce soit significatif, et on aura forcément des déviations parce que l'optique n'est pas parfaite, on a des transmissions ou des réflexions parasites, du bruit, des différences dans les détecteurs... Mais bon, en modifiant les angles relatifs, on peut observer une courbe qui ressemble à ça :
Les inégalités de Bell
Si on suppose qu'il existe une variable cachée qui permette aux deux photons de se mettre d'accord, alors cela a une implication sur le calcul des probabilités. Et Bell a démontré qu'il existait une différence entre les probabilités prédites par la mécanique quantique et celles prédites par l'existence d'une variable cachée.
Ça ressemble à ça :
On tient donc un outil pour savoir s'il existe une variable cachée ou si la mécanique quantique est juste. On sait aussi qu'il faut regarder du côté de 22.5° pour voir un maximum de différences et ceux qui regardent uniquement à 0°, 45° et 90° se font avoir dans les grandes largeurs.
Bell avait synthétisé cela sous la forme d'inégalités à respecter, avec des conditions particulières que je passe sous silence ici, c'est déjà assez compliqué comme ça, on fera confiance à ceux qui savent calculer. Vous pouvez aussi chercher sur le web le détail, ce n'est pas si compliqué que ça.
Et le vainqueur est ...
Évidemment, la mécanique quantique. Alain Aspect a démontré cela avec ce montage au siècle dernier, avec une confiance énorme (~40 écart-types).
Conclusion : pas de variable cachée, pas de transmission d'info plus rapide que la lumière, mais c'est sûr, on a une interaction non locale. Et inexpliquée.
On retiendra de cette expérience le coup de l'orientation des angles : on voit qu'on peut faire varier les probabilités avec un choix astucieux de chaque côté. Alice et Bob vont pouvoir s'amuser avec ça pour ce qu'on appelle la cryptographie quantique.
Sauf que.
Il existe des échappatoires
Par exemple, les photons pourraient "savoir" que les cubes séparateurs ont telle ou telle orientation avant de partir, et que ces fourbes se mettent d'accord sur une stratégie (secrète)
Il vaudrait mieux choisir la position des cubes de manière aléatoire (personne ne connait à l'avance l'orientation) APRÈS que les photons se soient séparés, et trop éloignés l'un de l'autre pour communiquer à une vitesse sub-luminique (paranoïaque avant tout).
On a donc intérêt à éloigner autant que possible tous les éléments. On notera les heures d'arrivée, puis on comparera plus tard, en rassemblant les données à une vitesse plus faible que la lumière, certes, on ne sait pas faire autrement.
Et puis il pourrait exister des corrélations liées à la circuiterie électronique qui vont aux détecteurs.
Alors on a réalisé une expérience plus convaincante, très différente du point de vue pratique.
Un test bien séparé
(vous pouvez sauter ce petit chapitre, et passez à l'expérience)
Une forme de test encore plus convaincante est de séparer les éléments (pas avec une source commune de photons comme précédemment). La forme dite "CHSH" (des noms de ses auteurs) est la suivante :

On met 0 ou 1, aléatoirement (c'est notre volonté propre de choisir ce qu'on veut) en entrée de chaque boite A et B, et sort +1 ou -1 en sortie. On enregistre les signaux d'entrée et de sortie ainsi que la date, comme ça on pourra vérifier les corrélations après coup.
Les boites sont suffisamment éloignées, plus loin que ne le permet la vitesse de la lumière pour communiquer, comme ça on est certain qu'il n'y a pas de compromission.
Bell nous a dit que si la physique est locale (vitesse de la lumière est le max) et réaliste (les propriétés sont définies au début et indépendantes de toute observation), alors on observera une corrélation plus importante que dans le cas de la physique quantique.
L'inégalité de Bell prend la forme suivante (un poil compliqué, je sais) :
Espérance du produit (x.y) pour a=0, b=0
+ Espérance du produit (x.y) pour a=1, b=0
+ Espérance du produit (x.y) pour a=0, b=1
- Espérance du produit (x.y) pour a=1, b=1 ≤ 2 (attention à la soustraction)
Si on met dans chaque boite un électron avec un spin, et qu'ils sont intriqués, alors la mécanique quantique prévoit une valeur de 2√2: on viole l'inégalité de Bell.
Pour éviter d'éventuelles échappatoires, sur une idée de Bell lui-même, on ajoute une boite au milieu :
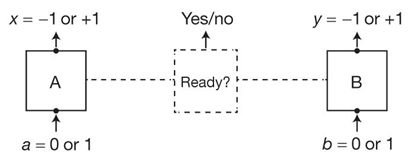
Le test "ready" permet de savoir si les deux boites ont été positivement intriquées, pour exclure du calcul les cas où l'intrication n'a pas marchée, éliminant "du bruit".
Test/mesure de Bell
et échange d'intrication
Lorsque l'on effectue un test de Bell, par exemple entre deux photons déjà intriqués, alors l'intrication "remonte". Le test est celui proposé juste ci-dessus. Comment fait-on cela ?
Vous retrouverez aussi la mesure de Bell dans les pages relatives aux qubits.
Une mesure de Bell partielle sur des photons intriqués peut se faire avec une simple lame semi-réfléchissante :
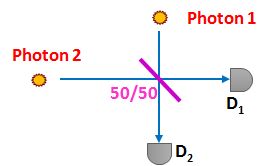
Si deux photons arrivent sur la lame, de chaque côté et en même temps, et présentent la même longueur d'onde et la même polarisation, alors on a une interférence destructive et un seul détecteur réagira. À ce moment-là, les deux photons sont indiscernables et intriqués. C'est pareil tant que les photons sont symétriques.
Par contre, s'ils sont dans un état antisymétrique, on retrouvera un photon sur chaque détecteur.
Avec deux photons polarisés verticalement ou horizontalement, il existe 4 cas, ce sont les 4 états de Bell. Un seul cas est antisymétrique, et c'est ce que l'on détectera si les deux détecteurs réagissent (25% des cas).
La mesure est partielle car on ne détecte qu'un seul des cas 4. On améliore les choses en ajoutant des cubes séparateurs de polarisation, mais ce n'est pas parfait quand on ne dispose que d'optique linéaire.
Échange d'intrication
Avec une mesure de Bell, il est possible de provoquer un échange d'intrication (swap). Pour cela, les deux photons doivent être intriqués chacun de leur côté avec un autre qubit. C'est ce qui sera réalisé juste après, à Delft.
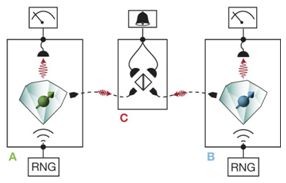
Nous avons deux boites quantiques A et B qui contiennent un qubit. Un photon est intriqué avec A, et un autre avec B, et sont dirigés vers la lame semi-réfléchissante en C où ils interfèrent ─ou pas.
Si un seul détecteur réagit, il y a eu intrication. Dans ce cas les deux boites quantiques A et B deviennent intriquées.
Instantanément. Non localement. Plus vite que la lumière. Sans que les qubits originaux ne se soient jamais rencontrés.
Nous avons donc là le moyen de savoir s'il y a eu intrication, et garder ou pas le résultat dans une expérience. Notez que la mesure détruit les photons.
On a suivi le conseil à la lettre à Delft
Le montage précédent a été réalisé à Delft. Nous avons les 3 éléments : deux boites quantiques A et B, et le test "ready" C. Ces trois éléments ont été éloignés les uns des autres pour éviter toute propagation de signal subluminique.
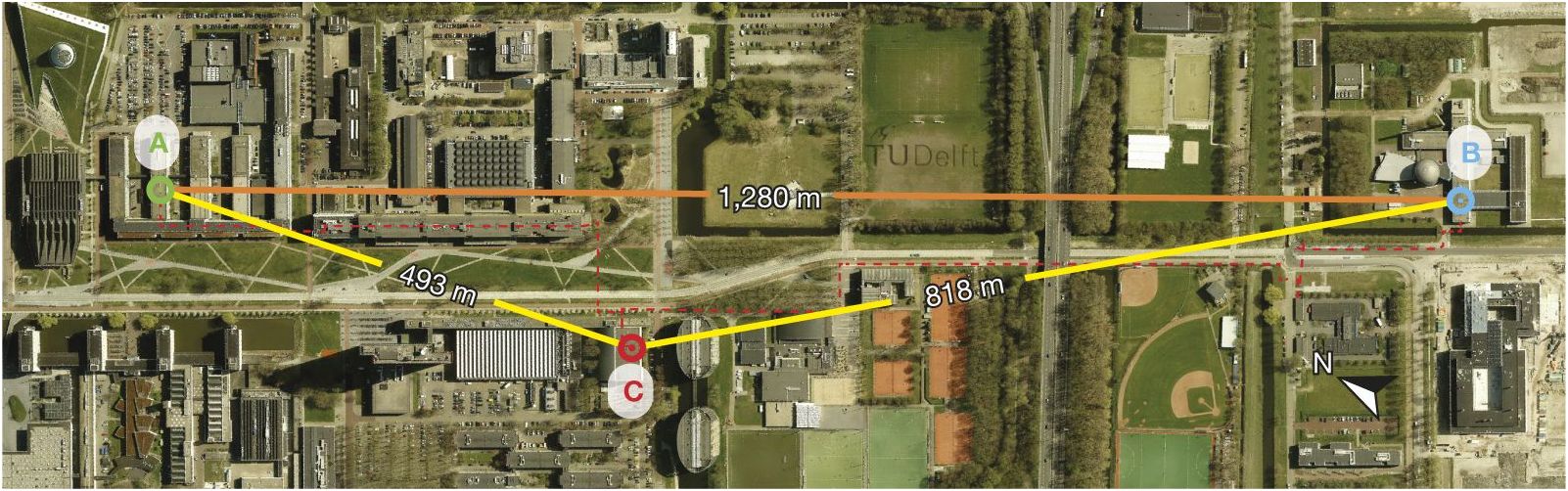
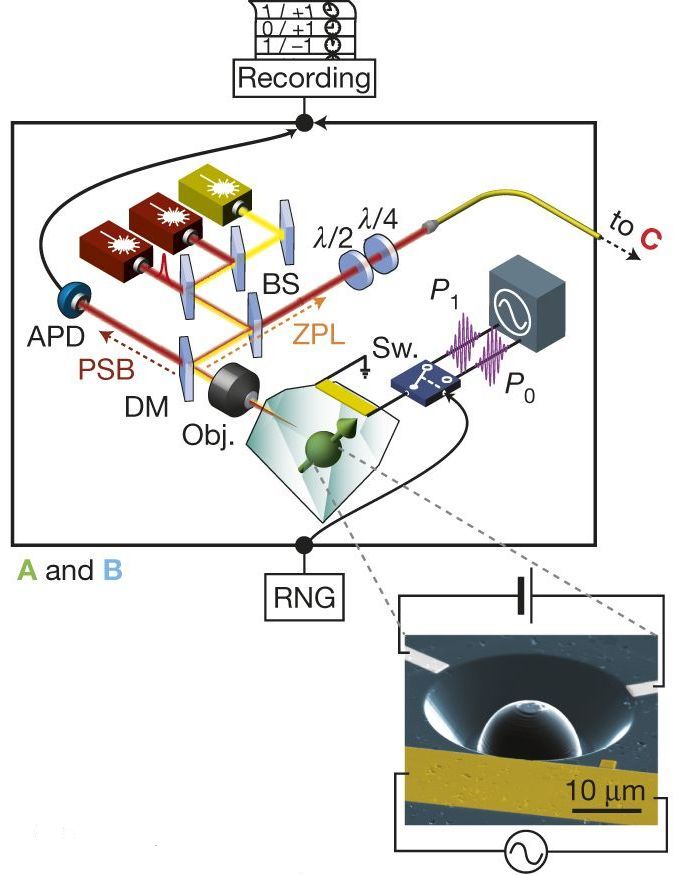
L'élément quantique est un électron piégé dans un défaut cristallin (dit NV) d'un diamant refroidi à 4K. On l'excite à l'aide de micro-ondes, et le spin est initialisé par pompage optique.
On lit le spin par excitation résonnante:
- Si le spin = 0, ca émet des photons => +1
- Si le spin = ±1, ça reste noir => -1
Mais avec ça, il n'y a pas d'intrication, évidemment, ils vivent leurs vies indépendamment. Il faut donc les aider. C'est là qu'on ajoute un élément en C.
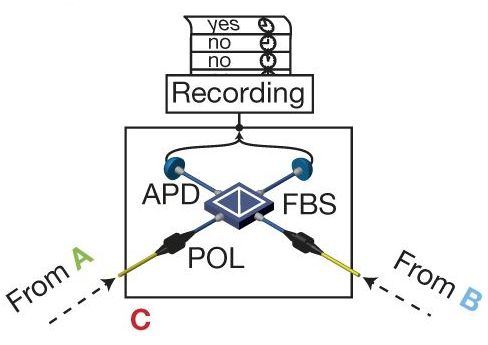
Quand les photons arrivent tous les deux en C, on les fait interférer avec la lame semi-transparente. Si on ne les distingue pas, l'observation provoque l'intrication maximale dans A et B, et ça sert aussi de détecteur "ready". Si on les distingue, on jette le résultat, il n'y a pas eu intrication.
La mise au point de l'ensemble, avec les générateurs de nombres aléatoires et consort, n'est certainement pas simple, l'intrication se produit avec une probabilité assez faible et il a fallu 220 heures d'observation pour voir 245 évènements.
Et ils ont trouvé 2.42 au lieu de 2, avec une erreur de 0.02.
Aucune hésitation possible concernant le résultat, c'est plié.
Conclusion
- Les inégalités de Bell sont violées (ce qui implique que l'on exclut les théories à variables cachées locales, plus clairement les théories aux variables aléatoires partagées) ;
- Il n'existe donc pas de variables cachées locales (dans le sens de créées localement, avant d'être séparées entre les participants), contrairement à ce qu'espérait Einstein ;
- Si l'on veut conserver l'hypothèse d'une limite à la vitesse de transmission d'une information (c, vitesse de la lumière), sans quoi les principes de relativité et de causalité relativiste seraient violés, il faut admettre que deux particules créées conjointement, même géographiquement séparées, continuent à se comporter comme un système unique (non-localité du système) dès lors qu'elles sont dans un état intriqué.
C'est fantastique. On n'y comprend rien, il faut avaler quelques couleuvres, mais c'est fantastique.
Bonus : Violation de Bell à 4 photons GHZ
J’ai trouvé cela encore plus convaincant que la première expérience d’Aspect. En voici une description légère. Quoique car il faut avoir vu ce qu'est une base de lecture en mécaQ. Mais bon, vous pouvez sauter cette section.
L’expérience est conçue ainsi :
- 2 paires de photon intriqués sont créés via un cristal BBO, générant environ 20000 paires intriquées par seconde, avec un petit délai réglable. Les pulses font 200 fs.
- Les lames quart d’onde et les polariseurs permettent d’analyser les photons en détectant leur coïncidence.
- Sur D1 et D4, on a l’analyse d’un photon de chaque paire.
- Les deux autres vont interférer dans le cube polarisateur PBS, ce qui les intriquera, et on aura alors nos 4 photons intriqués.
- Les deux sorties du PBS sont analysées de la même manière.
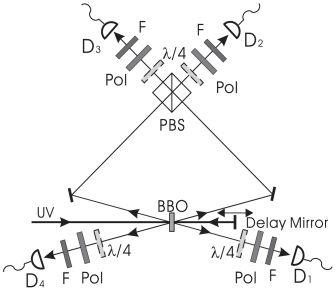
Voilà, nous avons notre matériel d’expérimentation, finalement plutôt simple.
Avec les lames quart d’onde et les polariseurs, on va pouvoir trier les polarisations. On peut observer directement des coïncidences HVVH et VHHV, mais pour être sûr qu’on a l’intrication, on va observer plutôt sur la base:
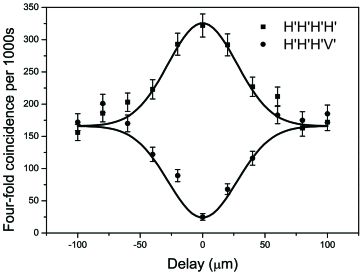
On compare alors H’H’H’H’ (intrication parfaite) et H’H’H’V’ en faisant varier le délai: le pic montre la superposition cohérente des photons.
On peut aussi considérer une autre base définie ainsi:
Notez la partie imaginaire: cela signifie que l’on a affaire avec une polarisation circulaire droite R ou gauche L.
On analyse alors certaines combinaisons qui sont des lectures des polarisations H’, V’ sur les photons 1 et 2, et R,L sur les photons 3 et 4. Parce qu’il existe certaines commutations particulières, seules quelques configurations (par exemple H’H’RR) sont observables pour chacune des 3 combinaisons.
Ces configurations sont analysées et on calcule leur probabilité d’apparition en prenant en compte une possible variable locale, ou alors la mécaQ (comme pour le test d’inégalité de Bell).
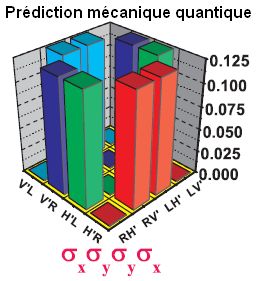

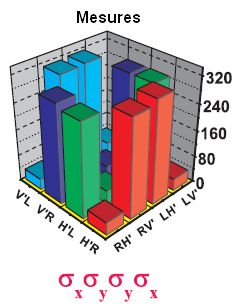
Yapa photo. La mécaQ gagne facilement. Au passage, on peut voir les corrélations sévères qui existent pour certains états.
Largué(e) ? il faudra alors suivre le cours sur la notation de Dirac.