Intro à la mécanique quantique
Les expériences précédentes ne tranchent pas si on a affaire à une onde ou une particule. On a voulu aller plus loin : est-ce qu’on peut faire des interférences avec un photon unique ?
Pour ça, on va utiliser un interféromètre de Mach-Zehnder. C’est une ruse où on recombine les chemins optiques.
Interféromètre de Mach-Zehnder
Comment on construit un tel interféromètre ? D'abord, on fait comme dans l'expérience précédente, mais sans les fentes.
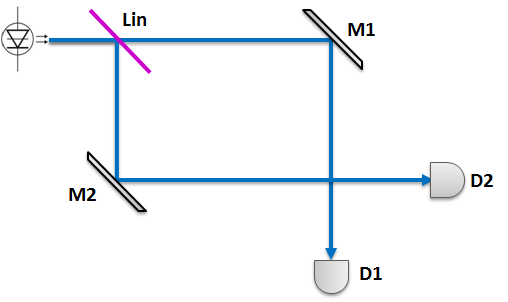
On crée deux chemins optiques possibles après la première lame semi-réfléchissante. La moitié des photons ou de l'intensité lumineuse ira d'un côté, et l'autre moitié sur l'autre chemin.
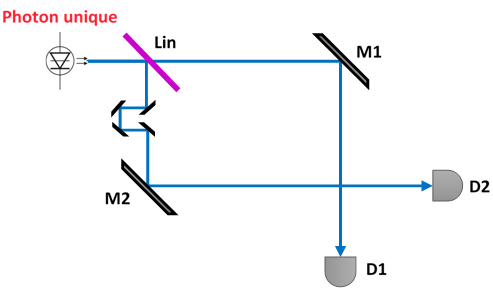
Deux miroirs permettent de réfléchir les photons pour les faire se "croiser". On met deux détecteurs de photon unique, un sur chaque chemin.
Vous me voyez venir : c'est exactement la même expérience que précédemment, c'est juste le montage qui est poil différent. Allez, je vous remets le schéma pour comparer, sans les fentes.
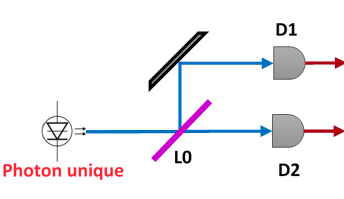
C'est quasiment la même chose, et on obtient le même résultat.
Mais on va ruser : on ajoute une lame semi-réfléchissante au croisement.
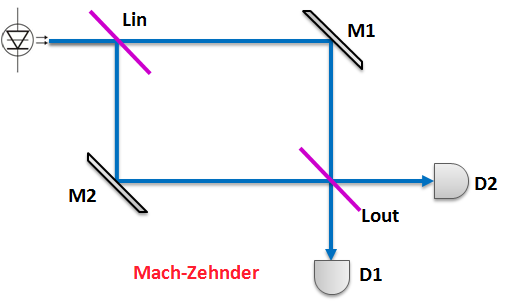
Lorsqu'il s'agit d'ondes, des interférences se produisent au niveau de la seconde lame, interférences du même tonneau que les fentes d'Young vues auparavant.
Une subtilité cependant ici : un paramètre important est la différence de marche entre les deux chemins optiques.
Ici, le montage est totalement symétrique, aussi la différence de phase est nulle : le chemin est identique des deux côtés.
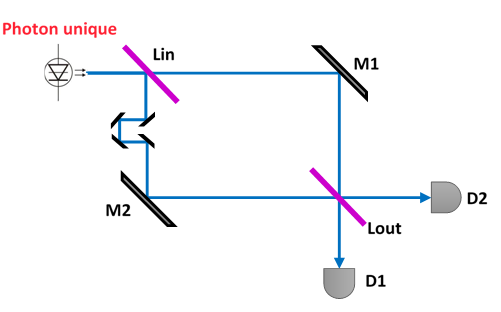
En faisant varier la distance parcourue à l'aide des 4 petits miroirs supplémentaires sur le chemin M2, on va faire varier le déphasage de l'onde par rapport à l'autre chemin si c'est une onde.
Sans la lame semi-réfléchissante
Mais bon, pour commencer, on enlève la seconde lame semi-réfléchissante, histoire de vérifier ce qui se passe sans les complications des éventuelles interférences.
On comptabilise le nombre de photons détectés sur D1 et D2, sur une dizaine de secondes, il suffit noter les heures d'arrivée sur chaque détecteur, tout en faisant varier la longueur du chemin optique du côté M2.
Voici le résultat obtenu, rouge d'un côté, bleu de l'autre, en fonction de la longueur du chemin optique additionnel ajouté avec nos 4 petits miroirs.
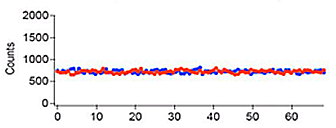
Rien de bien surprenant : que des anti-coïncidences -il n'y a jamais deux photons détectés en même temps (en tenant compte du chemin parcouru)-, et varier la longueur du chemin optique du côté M2 ne change rien.
Avec la lame semi-réfléchissante
On ajoute à présent notre lame semi-réfléchissante : notre interféromètre de Mach-Zehnder est alors complet.

Et on recommence l'expérience, toujours en faisant varier la longueur du chemin optique.
Voici le résultat :
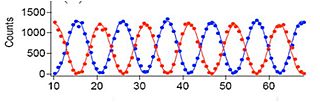
Oui, reprenez un cachet.

Rappelez-vous : ce sont des photons "un par un".
On constate un comportement ondulatoire, ce qui parait totalement extraordinaire, car on pourrait s'attendre à des évènements totalement indépendants, puisqu'il s'agit de photon "séparés".
Mais non, non seulement cela laisse la désagréable impression que les photons se rappellent ce qui s'est passé auparavant (vu le déphasage de 180 degrés entre les deux détecteurs), et se comportent comme une interférence, comme si un photon avait parcouru les DEUX chemins à la fois, et avait interféré avec lui-même.
C'est carrément extraordinaire.
Mais ce n'est pas le pire. Parce qu'on a tenté d'être plus malin que le photon. Et qu'on s'est pris une claque.