Les ordinateurs quantiques
qubit : reboot

Une mesure de Bell est une mesure qui permet de vérifier une intrication, cela peut être utile en cryptographie par exemple. Nous avons déjà vu cela quand on a voulu prouver la non-localité de l'intrication, et aussi avec les histoires de téléportation quantique.

Ici, on veut juste voir la même chose avec le formalisme de Dirac. Et on utilise alors une base orthonormée adaptée, pour avoir un état de Bell

État de Bell : état maximalement intriqué

C'est une base orthonormée qui permet de mesurer le maximum de violation des inégalités de Bell.

Par exemple, pour 2 particules A et B à 2 états 0 et 1, donc un total de 4 états :

|Φ+⟩ = 1/√2 [ ( |0A⟩ ⊗ |0B⟩ ) + ( |1A⟩ ⊗ |1B⟩ )
|Φ–⟩ = 1/√2 [ ( |0A⟩ ⊗ |0B⟩ ) – ( |1A⟩ ⊗ |1B⟩ )
|Ψ+⟩ = 1/√2 [ ( |0A⟩ ⊗ |1B⟩ ) + ( |1A⟩ ⊗ |0B⟩ )
|Ψ–⟩ = 1/√2 [ ( |0A⟩ ⊗ |1B⟩ ) – ( |1A⟩ ⊗ |0B⟩ )

On constatera la symétrie.

On verra plus tard que ça se crée avec une porte de Hadamard suivi d'un CNOT.

Il existe aussi l'état de Greenberger-Horne-Zeilinger (GHZ), un état intriqué à au moins trois particules, et aussi l'état W. C'est juste pour dire qu'il existe diverses définitions.

Mesure de Bell

Mesure de Bell ou BSM Bell State Measurement en anglais.

En téléportation quantique, il avait fallu intriquer un photon dans un état inconnu avec un autre photon intriqué pour transmettre l'état sans le lire directement, et on avait alors fait une mesure de Bell.

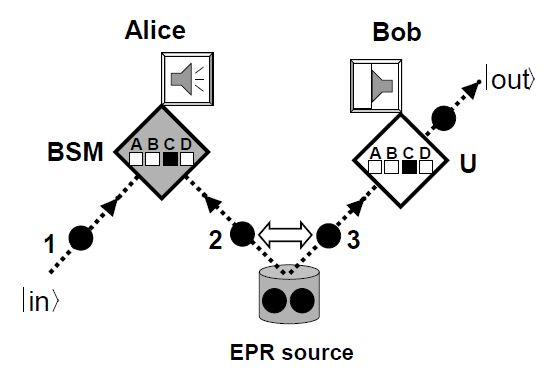
teleportation quantique

Évidemment que la mesure (A,B,C,D) correspond aux 4 états de Bell.

Comment fait-on cela avec des photons polarisés ? Eh bien nous avons 4 possibilités, pour rappel :

|Ψ> = αHH |H1H2⟩ + αHV |H1V2⟩ + αVH |V1H2⟩ + αVV |V1V2⟩

Les 4 états de Bell correspondants, en notation de feignasse :

|Φ+⟩ = 1/√2 [ ( |H1H2⟩ ) + ( |V1V2⟩ )
|Φ–⟩ = 1/√2 [ ( |H1H2⟩ ) – ( |V1V2⟩ )
|Ψ+⟩ = 1/√2 [ ( |H1V2⟩ ) + ( |V1H2⟩ )
|Ψ–⟩ = 1/√2 [ ( |H1V2⟩ ) – ( |V1H2⟩ )

Nous avons alors 4 nouveaux vecteurs, orthogonaux, qui définissent une nouvelle base de mesure.

La mesure des 4 états de Bell est généralement difficile. Mais on peut faire une mesure partielle facilement, par exemple avec une simple lame semi-réfléchissante.

lame semi-réfléchissante

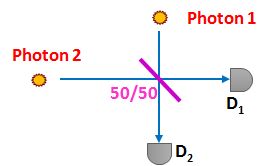
Seul l'état |Ψ–⟩ donnera une coïncidence sur D1, D2. Pour les 3 autres états, les deux photons sortent du même côté. Il est (évidemment) impératif que les deux photons arrivent en même temps sur la lame semi-réfléchissante pour produire des interférences (ce qui permet accessoirement de régler l'appareil, puisqu'on aurait des photons 50/50 de chaque côté sinon).

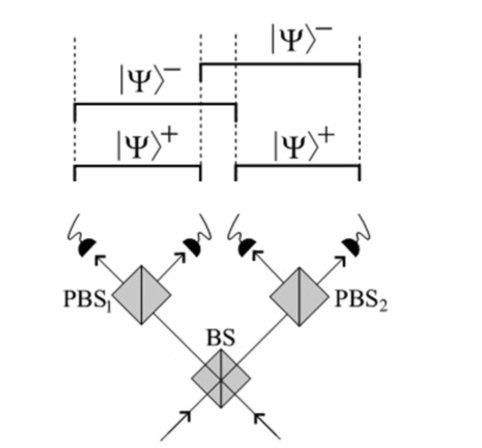
mesure bell à cube polar

On peut faire mieux en utilisant des cubes séparant la polarisation après la lame semi-réfléchissante, mais la mesure est toujours incomplète en fait. On distingue |Ψ+⟩, |Ψ–⟩ (la moitié des cas) mais pas |Φ+⟩, |Φ–⟩ (pour le cas des photons).

Avec les techniques linéaires (lame, cube séparateur...), on ne peut décoder que 3 états au mieux. Il faut des trucs bien plus compliqués pour aller plus loin.

Codage superdense

Comme il existe 4 cas, on peut coder 2 bits d'information classique avec deux qubits intriqués, c'est le superdense coding.

Alice, à partir d'un qubit basique |Φ+⟩, appliquera une des 4 transformations :

  1. l'identité, autrement dit rien, pour |Φ+⟩
  2. un retournement de phase Z pour obtenir |Φ–⟩
  3. un NOT (X) pour obtenir |Ψ+⟩
  4. un XZ pour avoir |Ψ–⟩

Puis Alice envoie le qubit préparé à Bob qui devra faire une mesure de Bell pour le décoder.


Des montages plus complexes ont été proposés pour aller plus loin, mais c'est visiblement la zone (on ne peut pas distinguer les 4 cas en utilisant uniquement des transformations linéaires).