Les ordinateurs quantiques
qubit: reboot

En fait, c'est assez simple car il s'agit d'espaces vectoriels et d'algèbre linéaire, avec des matrices plus ou moins cachées derrière le formalisme. On a commencé à le faire avec des nombres complexes, sinus, cosinus et l'équivalent en exponentielle imaginaire ben oui ces trucs que vous n'aimiez pas trop à l'école.

Un qubit, ça peut être n'importe quoi, un chat célèbre par exemple. D'ailleurs une difficulté de la mécaQ est de bien choisir ce qu'on manipule, car dès lors qu'on veut que ça interfère avec l'environnement, alors il faut introduire cet environnement. Et quand deux qubits se rencontrent, ça devient prise de tête quand on n'a pas l'habitude.

Le qubit est l'élément d'information minimal. Par principe inutile de chercher une raison physique il est constitué de deux états superposés :

• souvent notés |0⟩ et |1⟩
• mais on peut aussi utiliser |chat vivant⟩ et |chat mort⟩
• ou encore, pour la polarisation d'un photon, horizontale ou verticale |H⟩ et |V⟩, ou |→⟩ et |↑⟩

C'est juste la désignation des deux états possibles. C'est comme ça.

Le qubit est représenté par son vecteur, qui interviendra dans la fameuse fonction d'onde, et comme tout vecteur, il s'exprime en fonction de la base constituée par les deux états :

Mais si, à l'école, vous utilisiez :

avec (x,y) la position du point dans le plan. C'est une décomposition sur une base orthonormée. C'est pareil.

Bra-ket : c'est la notation de Dirac, universellement utilisée pour les histoires de qubit.

|Ψ⟩ est un vecteur colonne (vertical) avec α et β : c'est un ket .

⟨Ψ| est son conjugué (mathématique), c'est le bra et pas de bra, pas de chocolat. C'est un vecteur ligne (horizontal) avec les conjugués α* et β* (pour rappel le conjugué d'un réel est identique, et pour un complexe a+bi, c'est a-bi ).

Ce vecteur va nous donner une probabilité d'avoir l'état |0> ou |1>, via le module, donc le carré, et on doit avoir forcément la propriété dite condition de normalisation :

Autrement dit, sa norme est 1, le vecteur est toujours de longueur 1. La probabilité totale est forcément 1, on est sûr de détecter le photon.

Là où ça devient sportif, c'est que les coefficients sont des nombres complexes. Dans ce cas, on n'est plus dans un espace vectoriel simple, mais dans un truc plus gros que les matheux appellent un espace de Hilbert et ça fait super-bien dans la conversation.

Et ce sera encore plus frime si vous dites que non, comme ça, ce n'est qu'un espace de Banach, il lui faut une base orthonormée pour qu'il devienne Hilbert, vous pourrez alors encore plus frimer.

Vient le problème de représenter un vecteur avec des nombres complexes. Dans les réels, c'est tout simple, c'est un plan. Mais là, on n'a pas deux réels mais quatre réels : 2 amplitudes + 2 phases.

Eh bien nos matheux ont trouvé le moyen de faire un truc qui parait bizarre au premier abord: les deux vecteurs |0⟩ et |1⟩ seront placés dans un espace à 3 dimensions, tête-bêche (un vers le haut, l'autre vers le bas), tout ça parce que le module vaut toujours 1, et donc notre vecteur pourra se balader dans une sphère dite sphère de Bloch et re-paf, cette fois vous êtes un spécialiste de la mécaQ et c'est plus chauvin si vous parlez de sphère de Poincaré lui au moins, il est français.

Ça aide à se représenter visuellement le bouzin :

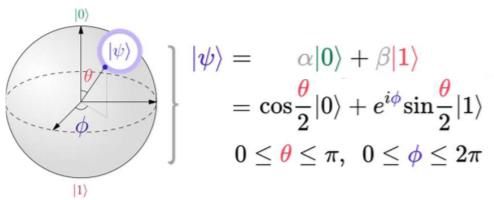
Et là, vous avez les nombres complexes + les sinus et cosinus qui apparaissent immanquablement avec les angles. Pour rappel, la formule d'Euler : e ^{i Φ} = cosΦ + i sinΦ

Pour rappel : vous devez choisir votre base orthonormée.

Ici la base a été choisie par rapport au système de mesure, son angle de polarisation c'est { |→⟩ , |↑⟩ }

Mais on peut choisir une autre base orthonormée, en diagonale { |+⟩ , |–⟩ }, avec

Avec les problèmes de calcul liés au changement de base mais ça ne sera pas aussi pénible que de passer en notation polaire.

C'est une définition utile pour les polarisations diagonales, utilisée en transmission d'information. Dans ce cas, un photon |→⟩ pur, qui aurait donné 100% de détection sur un détecteur H, donnera du 50/50 sur une détection en diagonale. Il est vu comme un état superposé.