Les ordinateurs quantiques
L'informatique quantique

La porte CNOT est une porte dite conditionnelle ou contrôlée. Si la condition (= le premier qubit) :

• est nulle, à |0⟩, alors le second qubit est inchangé
• est vraie, à |1⟩, alors le second qubit est inversé

Autrement dit :

1. |00⟩ ⇒ |00⟩ : inchangé
2. |01⟩ ⇒ |01⟩ : inchangé
3. |10⟩ ⇒ |11⟩ : le second qubit est inversé : 0 est devenu 1
4. |11⟩ ⇒ |10⟩ : le second qubit est inversé : 1 est devenu 0

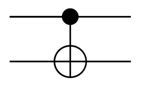
La matrice correspondant au CNOT est simple : le premier carré est l'identité, et le dernier est un échange Pauli-X pour ceux qui ont fait attention juste avant. Mais qu'on ne s'y trompe pas, cela ressemble beaucoup au SWAP, on a simplement un échange de 2 coefficients, les deux derniers:

En entrée : |Ψ⟩ = α₁ |00⟩ + α₂ |01⟩ + α₃ |10⟩ + α₄ |11⟩

En sortie : |Ψ⟩ = α₁ |00⟩ + α₂ |01⟩ + α₄ |10⟩ + α₃ |11⟩

On peut généraliser cette histoire de porte contrôlée avec n'importe quelle fonction.

CNOT a l'air simple comme ça, au premier abord, mais il existe des implications oiseuses.

Pour bien se rendre compte de ce qui se passe, il faut faire une simulation complète (avec les mains), et nous allons prendre un exemple particulier que nous allons décortiquer.

Nous allons reprendre notre premier qubit à |0⟩ suivi d'une porte de Hadamard, et rien sur le second qubit —il reste à |0⟩—, suivi de notre porte CNOT où le qubit du haut sert de contrôle :

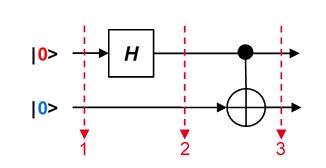
Calculons la fonction d'onde de l'ensemble à chaque étape :

1. |Ψ⟩ = |00⟩ évidemment, c'est l'initialisation.
2. Hadamard en haut ⊗ l'identité en bas.
   |Ψ> = (1/√2 |0⟩ + 1/√2 |1⟩ ) ⊗ |0⟩ = 1/√2 |00⟩ + 1/√2 |10⟩
   On n'observe jamais l'état |1⟩ sur le second qubit, normal, il n'a pas changé. Le vecteur est ( 1/√2 , 0, 1/√2, 0 )
3. Appliquons la matrice CNOT à notre vecteur.
   Il devient ( 1/√2, 0, 0, 1/√2 ), puisqu'on échange les deux derniers termes (dans le swap, c'était les termes du milieu, rappelez-vous). La fonction d'onde devient:
   |Ψ> = 1/√2|00⟩ + 0|01⟩ + 0|10⟩ + 1/√2|11⟩ = 1/√2( |00⟩ + |11⟩ )
   Au passage, vous avez vu l'évaluation d'une condition, vous ?

On peut faire le même calcul avec des matrices, en notant qu'un simple fil DOIT être remplacé par la matrice identité. On notera qu'en augmentant le nombre de qubits, nos matrices vont vite devenir démentielles (quand on atteint entre 50 et 60 qubits, on est obligé de jeter l'éponge côté calcul classique).

Comparons avec la porte Hadamard et NOT simplement en parallèle, qu'on avait calculée précédemment :

Les différences sont simples concernant la matrice 4x4 : les deux premières lignes sont "échangées", et c'est tout. Rappelons que les deux qubits travaillent "chacun de leur côté" quand ils sont parallèles, ce qui n'est pas le cas pour la porte CNOT -a priori- où on pourrait bien observer des corrélations particulières.

Eh bien c'est le cas.

Nous constatons que nous avons une probabilité de 50% d'observer |00⟩ et 50% d'observer |11⟩. On observe toujours le même résultat sur les deux qubits. Cela n'a rien de bien étonnant quand on y pense: on s'est quand même arrangé pour garder |0⟩ si on avait |0⟩ au contrôle de la porte, et inverser pour avoir |1⟩ si on avait |1⟩ quand on discute "condition" et qu'on utilise la définition proposée pour cette porte CNOT.

Mais le résultat est plus subtil.

On ne sait pas si c'est zéro ou un, mais à coup sûr, ils seront identiques. Alors que les deux qubits sont à présent séparés ! Ils peuvent continuer à vivre leur vie séparément du point de vue physique, mais quand même, ils seront liés, sans limitation de localisation et de temps. Ce qui devrait vous rappeler quelque chose: c'est le phénomène d'intrication.

Si on continue à faire d'autres opérations, cette corrélation se poursuivra, mais on ne connaitra pas sa valeur tant que la mesure ne sera pas faite. Ça n'a l'air de rien, mais cette intrication n'a pas d'équivalent classique. Ce n'est pas le cas pour la mise en parallèle des 2 qubits : c'est seulement si on fait interagir deux qubits que des phénomènes inhabituels se produisent. Mais ça ne se voit pas facilement.