Tous ces sites qui tentent de vous expliquer, ou croient dur comme fer vous expliquer ce qui se passe, sont légion. Je n'ai pas pris le temps d'écouter des vidéos, car si on n'est pas capable de l'écrire, et bien on va perdre son temps.
Je vais canarder en règle, parce que les explications fournies sont souvent au mieux des copies d'autres avis, montrant que ces auteurs n'ont pas vraiment réfléchis à ce qu'ils écrivent, au pire des inepties.
C'est la partie amusante pour moi, j'aime râler.
Mais en fait, vous pouvez sauter cette page si vous venez pour avoir mon explication. C'est en quelque sorte "l'état de l'art" des explications.
Pierre Spagnou
Commençons avec un site sérieux, celui que j'ai donné en référence pour l'expérience de Hafele et Keating :
- L’expérience cruciale de Hafele et Keating une analyse par Pierre Spagnou.
Pierre Spagnou recueille et commente par le menu les avis des contradicteurs, et quand je suis tombé sur son excellent site, je me suis dit que j'allais enfin trouver l'explication qui me manque.
La figure 4 et ses commentaires sont instructifs, mais on reste sur sa faim ! Ce sont des affirmations ─certes exactes─ sans aucune justification.
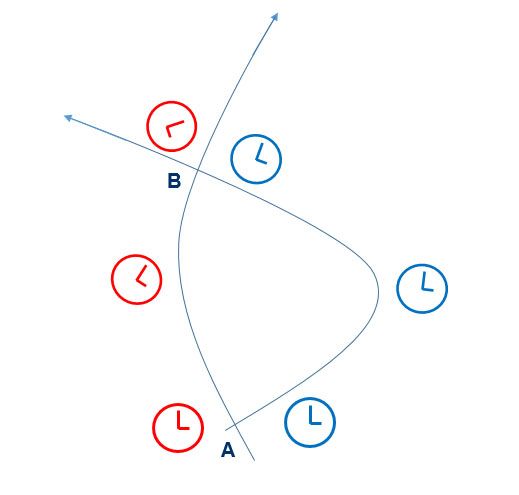
Désynchronisation des horloges parfaites. Les deux horloges identiques sont synchronisées au départ (point A) mais ne le sont plus à leur point de rencontre (point B) à l’issue de leurs trajectoires respectives, chacune ayant enregistré un temps propre (cumulé) différent.
Le temps propre est a priori spécifique à la ligne d’univers considérée. On peut donc imaginer des scenarios très divers[8] : un voyageur parti de A en même temps que son comparse peut arriver après lui en B tout en ayant mesuré une durée propre plus courte ; les deux voyageurs partis ensemble de A peuvent arriver séparément en B tout en ayant enregistré chacun la même durée propre. Ce qui est contraire au sens commun certes – mais presque banal dans le cadre novateur de la chronogéométrie einsteinienne.
Voilà qui est typique de la réponse de scientifiques. Pour eux, c'est normal, ça marche comme ça. Mais bon sang, mettez-vous au niveau des petites gens, et expliquez-leur où ils se trompent et pourquoi ! Certes, ce n'est pas l'objet de l'article, mais quand même, on est en plein dedans, un lien vers une explication ne serait pas de refus...
Ceci dit, je rends hommage à l'excellence de cet article. Impressionnant de précision.
Kikipedia
L'inévitable Wikipedia...
Assez étrangement, Wikipedia a le bon goût d'effectuer des catégories parmi les gens qui commentent ce paradoxe. Quatre classes sont définies, que je reprends ici :
- La classe AR: majoritaire. Ce sont qui acceptent.
J'en attends toujours une explication qui se tienne.
Et pas avec des diagrammes plus ou moins compliqués, qui ne sont souvent rien d'autre que l'application des équations. Ça, j'avais compris. Il n'y a que dalle là-dedans, vous ne pointez pas l'erreur de raisonnement.
- La classe OR: pas de modification du temps propre.
Ils ont un argument "kitu" : eh les gars, 99.99% du temps, le mouvement est rectiligne uniforme, et la dissymétrie interviendrait au moment de misérables accélérations ? Et qu'en plus, très souvent, vous dites négliger ? Va falloir trouver plus convaincant.
- La classe OG: on ajoute cette fois des périodes d'accélération plus ou moins intenses,
avec des résultats sur le vieillissement qui s'inverse suivant l'intensité.
C'est une tentative. Avec des résultats discutables. Ce serait quand même très étrange que cette phase d'accélération soit si cruciale pour cette histoire de dissymétrie entre les deux jumeaux. Ce doit être plus simple. (L'accélération est effectivement cruciale pour appliquer correctement la transformée du bon côté. Mais son intensité est secondaire.).
- La classe AG: la résolution se trouve dans la relativité générale.
Echappatoire surprenante, la relativité générale n'a d'impact que si la gravitation intervient. Et on peut l'éliminer facilement dans cette expérience par la pensée.
Puis viennent les explications. Visiblement un conglomérat de ce qui existe, même si cela semble plus ou moins rangé.
Un intérêt est que la plupart des articles sur le sujet tombent plus ou moins dans ces explications, ce qui va me faciliter la tâche quand j'en parlerai plus tard.
Longueur des lignes d'univers
C'est l'explication la plus courante, pas forcément directement convaincante, mais elle est juste.
On vous explique que le temps propre dans un espace de Minkowski revient à suivre son chemin dans les 4 dimensions, et que dans tous les cas, le temps propre qui a suivi une ligne droite = aucune force appliquée est nécessairement plus long que n'importe quel autre chemin, les inégalités triangulaires marchant "en sens inverse" de ce que l'on a l'habitude d'avoir dans l'espace euclidien.
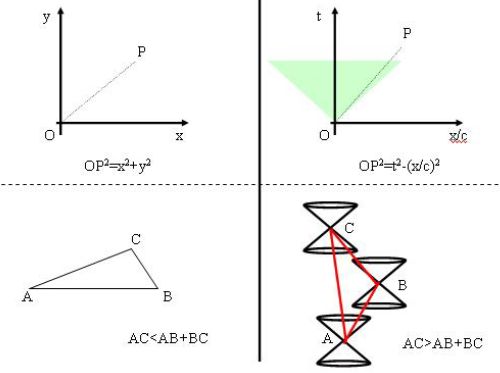
Le chemin le plus court devient le plus long...
Alors évidemment, le malheureux lecteur qui n'a pas l'agrégation de mathématique est largué, peu convaincu, vu que cette histoire est une conséquence de ce qui se passe à un niveau élémentaire physique, où la dissymétrie n'est pas expliquée.
Échanges de signaux et effet Doppler
L'astuce consiste à faire émettre par le voyageur des signaux à intervalles réguliers, par exemple toutes les secondes, suivant l'horloge locale. L'effet Doppler est une conséquence secondaire de la vitesse, en plus un décalage de la fréquence sera observé.
On dessine alors ce qui se passe sur des jolis diagrammes où on est assez vite perdu, et on se demande où on veut en venir.
(Images du site de Gérard Villemin, voir plus loin, je les trouvais plus claires.)
Ce qui parait être une explication n'en est pas une. La seule chose que cela peut montrer, à la rigueur et encore, c'est que le décalage temporel se manifeste déjà au niveau de la seconde.
Autrement dit, la différence de vieillissement est déjà présente au niveau d'une unité de temps assez petite devant le voyage complet.
C'est bien joli, mais si on admet que cette différence existe déjà au niveau d'une seconde, alors évidemment en accumulant sur la durée du voyage, ça va le faire !
Et au passage, si on admet déjà une disymmétrie au niveau de la seconde, alors l'accélération et autre demi-tour n'ont plus rien à voir...
Et la question à deux balles devient : OK, montrez-moi qu'il y a une différence de vieillissement sur une seconde. Et là, il y a moins de monde. Voire personne. Sauf moi ?
Ensuite, Wikipedia propose quelques raffinements secondaires, qui n'apportent aucun éclairage nouveau.
Accélérations
Wikipedia introduit les accélérations et freinages, requis pour faire le voyage. Et très justement indique que cela n'a qu'une influence secondaire, les calculs sont plus compliqués mais faisables.
Mais le fait d'avoir une accélération, requise pour que les jumeaux se retrouvent dans le même référentiel, provoque la dissymétrie.
Villemin
- Paradoxe des Jumeaux de Langevin / Paradoxe des horloges (clock paradox) / Le boulet de Jules-Verne Langevin / Villemin.
Un site d'un passionné des nombres, et aussi de la relativité, manifestement. J'ai récupéré son graphique pour illustrer le Doppler, ci-dessus.
Principe de l'explication
C'est le demi-tour qui est la cause de la non-symétrie de la situation des deux jumeaux. Avant et après le demi-tour, les phénomènes observés sont totalement symétriques, sans contradiction ni paradoxe, pourvu que l'on sache exactement de quoi l'on parle.
Ah là là ! Ce n'est certainement pas le demi-tour la cause. Comment croire qu'en faisant un demi-tour, alors c'est ce jumeau qui s'arrête de vieillir ?
Et en plus, s'il avait regardé d'un peu plus près le voyage, il se serait rendu compte qu'au moment du demi-tour, immanquablement le voyageur se retrouve dans le même référentiel que le sédentaire, et donc le problème de dissymétrie existe déjà à ce niveau. Le retour ne fait que doubler l'addition...
Il est alors nécessaire d'utiliser une notion de la relativité générale (Mouvement accéléré), pour intégrer le demi-tour du jumeau volant.
Là, il s'enfonce. Pas besoin de relativité générale, la gravitation n'intervient pas.
C'est malheureusement une attitude typique des gens qui tentent d'expliquer ce paradoxe. Ils croient avoir compris en fuyant en avant vers des choses plus complexes.
Gabrielle Bonnet / ENS Lyon
- [2003] Relativité et vitesse de la lumière / Gabrielle Bonnet, École Normale Supérieure de Lyon.
(Section "le paradoxe des jumeaux")
Si l'on applique rapidement les lois de la relativité restreinte à ce problème
...
Comme les jumeaux, à l'instant initial et à l'instant final,
sont au même instant au même endroit,
ils le sont encore dans tous les référentiels
et on ne peut pas invoquer des problèmes de simultanéité pour résoudre le problème.
Ce raisonnement est faux car, si le référentiel du jumeau resté sur Terre peut être considéré, en première approximation, comme Galiléen, celui du jumeau voyageur ne l'est pas : pour revenir à son point de départ, il ne peut pas avoir été constamment animé d'un mouvement rectiligne et uniforme, il doit forcément avoir fait demi-tour quelque part !
Le référentiel du jumeau voyageur n'étant pas Galiléen, la situation n'est pas symétrique, les deux référentiels ne sont pas équivalents.
Un grand classique : on donne une raison, mais on n'explique rien.
Pourquoi ne pas donner la solution en expliquant pas à pas ? A quel moment on dit "l'accélération provoque..."
Et même remarque à propos du demi-tour, où les deux se retrouve nécessairement dans le même référentiel, et donc le problème de dissymétrie existe déjà. Et permet de découper le problème en deux parties égales.
Pour calculer le temps écoulé dans chaque référentiel, il faut faire intervenir la relativité générale. On trouve que le jumeau voyageur est effectivement plus jeune que le jumeau casanier. Cette propriété a été vérifiée expérimentalement avec des horloges atomiques extrêmement précises...
La relativité générale. En voilà une qui n'a vraiment rien compris et qui essaye de l'expliquer.
Ici, seule la relativité restreinte doit servir, inutile de s'échapper en avant.
En voilà une qui n'a vraiment rien compris et qui essaye de l'expliquer.
Ici, seule la relativité restreinte doit servir, inutile de s'échapper en avant.
techno-sciences.net
- Paradoxe des jumeaux / techno-sciences.net
Évidemment, dans un site de ce genre, on se doit de traiter ce paradoxe. Ils annoncent la couleur : c'est du Wikipedia, manifestement arrangé. Eh bien ils n'ont pas fait semblant, la section "résolution" est longue comme un jour sans pain. C'est que ça doit être complexe.
(Dilatation du temps et erreur de raisonnement)
On ne peut donc considérer les transformations de Lorentz entre les deux repères d'Alain et Bernard ni considérer la dilatation du temps du point de vue du repère non inertiel de Bernard. Nous avons trouvé l'erreur de raisonnement qui induit le paradoxe.
Certes, mais alors, comment on fait ?
Plusieurs solutions sont proposées, pour faire bonne mesure.
Et là, on retrouve les solutions proposées dans Wikipedia.
- Le coup du diagramme de Minkowski. Et comme on ne peut pas mettre dans le référentiel de Bernard, la discussion est close. C'est nul, le gars qui a ré-écrit cela n'a rien compris.
- Puis on a le Doppler, qui n'explique rien, on l'a déjà vu chez Wiki.
Puis c'est un ramassis de bêtises sur les histoires de synchronisation et de vieillissement brusque lié à l'accélération et au demi-tour. Ceci dit, ça vaut son pesant de moutarde à lire.
Et brusquement, l'auteur revient au problème initial :
Pourquoi c'est Alain qui est inertiel et pas Bernard puisque le point de vue peut être totalement inversé ?
Un soupçon d'optimisme me traverse à ce moment-là ! Pour arriver à :
C'est la relativité générale qui est venue résoudre définitivement ce dilemme.
Alors là, on comprend que l'auteur n'a rien compris du tout, et que c'est un blaireau en relativité. Pas de gravité = pas besoin de la relativité générale, c'est pourtant simple. Puis ça noie le poisson avec l'effet Sagnac, mais au moins ce site a le bon goût d'aborder l'effet Sagnac dans une autre page. Sauf qu'ils n'abordent pas du tout l'expérience de Hafele et Keating, ce qui est étonnant vu qu'ils font le tour de la Terre, quand même.
Evitez ce site et ses explications oiseuses. Perso, rien ne m'a convaincu.
Artru
- [2012] Introduction à la relativité / Marie-Christine Artru (ENS Lyon) Xavier Artru (Institut de Physique Nucléaire de Lyon et Université Lyon 1).
L'Ecole Normale Supérieure : on pourrait s'attendre à de la pédagogie.
Le petit chapitre sur le temps propre et les jumeaux de Langevin, ça me parait un peu court.
Un malheureux diagramme suffit pour démontrer que tout va bien, que forcément le temps propre est plus court, avec une addition des deux demi-trajets ─alors que ça ne sert strictement à rien de faire ça puisque le voyageur revient forcément lors du demi-tour dans le même référentiel que le sédentaire, quand sa vitesse s'annule.
Le coup du temps propre est effectivement le cas, mais ce n'est pas comme ça que vous dézinguerez les arguments opposants.
Faites donc le même croquis de la même chose dans le référentiel du voyageur. Qui donnera EXACTEMENT le même résultat. Exactement le contraire. Puis indiquez où se situe l'erreur...
La dissymétrie entre les deux jumeaux provient du fait que le référentiel du jumeau voyageur a changé au point de demi-tour.
C'est malheureux, car c'est effectivement (une partie de) la bonne explication à mon sens, mais c'est suffisamment mal expliqué pour qu'un opposant ne puisse accepter l'argument. J'espère que je serai plus pédagogue.
Société Astronomique de France
- Paradoxe de Langevin / Société Astronomique de France - Commission Cosmologie.
Comme Wikipedia, mais un peu plus pédagogique, je trouve. D'abord le diagramme de Minkowski, puis le Doppler. Rien de nouveau par rapport à ce qu'on a déjà vu.
Puis ça se gâte avec la relativité générale. On tombe dans des argumentations oiseuses, c'est du n'importe quoi. C'est beaucoup plus simple que ça.
Les auteurs se rendent compte que leurs explications deviennent longuettes et donc suspectes. Ils donnent même la source de leurs informations. Ils se rattrapent à la conclusion. C'est déjà ça.
Marc Lachièze-Rey (CEA)
- [2010] La disparition du temps en relativité / Pour la Science / Marc Lachièze-Rey (CEA).
- [2010] La disparition du temps en relativité / article complet sur Cairn.info / Marc Lachièze-Rey (CEA).
Typique de l'article où on se sent petit ─la raison de la dissymétrie est évidente, voyons !
Le jumeau sédentaire n’a pas bougé (ou très peu) : sa ligne d’univers est une droite (en RR) ou une géodésique (en RG). Ce n’est pas le cas pour l’autre jumeau qui, pour partir puis pour faire demi-tour, a subi la poussée des moteurs de sa fusée : il a décrit une courbe compliquée dans l’espace-temps.
Que l’on traite le problème du point de vue de la RR ou de la RG, le résultat est le même : les deux jumeaux ont bien vécu des durées différentes.
Et on reste sur sa faim. Certes, l'auteur a raison, mais le raccourci est violent. Et donc peu convaincant.
Science Etonnante
- [2020] Le paradoxe des jumeaux / Science Etonnante / David Louapre.
Une vidéo suivie d'explications. L'auteur reprend les concepts habituels, et a beau aborder le changement d'observateur, je trouve qu'il s'emmêle un peu les pinceaux au moment du demi-tour avec ses lignes de simultanéïté.
Son explication de changement ne colle pas avec le fait qu'au moment du demi-tour, le voyageur a eu nécessairement une vitesse nulle dans le référentiel du sédentaire, et il s'est donc retrouvé dans le même référentiel. On peut alors comparer les horloges.
Surtout que comme je l’ai dit, la différence n’existe de façon absolue qu’une fois les jumeaux réunis.
Il manque la fin de la phrase "... jumeaux réunis dans le même référentiel", pas nécessairement au même endroit spatial. Et oui, ça change un poil l'explication à fournir.
Ceci dit, le sujet est plutôt bien traité, mais n'explique pas vraiment la raison de la dissymétrie, on reste sur sa faim.
Jean-Marc Lévy-Leblond
- [2011] Le paradoxe des jumeaux / Jean-Marc Lévy-Leblond.
Support d'une présentation faite à Fleurance en 2011.
La contradiction est abordée frontalement, mais JMLL ne met pas vraiment le doigt sur ce qui lève la contradiction. L'explication des différents chemins, les lignes d'univers, est par contre intéressante.
Bon, assez râlé. La critique est aisée, l'art est difficile. Mais je suis persévérant, et j'ai vraiment voulu comprendre. Et tenté de vous l'expliquer. Au risque de me prendre des boulets rouges comme ceux que j'ai osé balancer.