Loin de moi l'idée de vous faire une démonstration, mais juste vous donner une idée d'où vient la fameuse formule d'Einstein. En rappelant au passage la différence entre la masse et le poids, et en donnant un exemple pas courant.
Je vais simplement vous introduire la formule "à la Feynman".

Transformation de Lorentz
La vitesse c de la lumière ne saurait être dépassée et les lois de la physique restent les mêmes dans n'importe quel repère galiléen. On en déduit la transformation de Lorentz, où sont introduits le β et γ, qui servent à calculer les coordonnées d'un point depuis un repère vers un autre repère en translation uniforme à la vitesse v (le long de l'axe des x, histoire de se simplifier la vie) :
Passer du référentiel Alice (xa,ta) au référentiel Bob (xb,tb) :
│ xb = γ ( xa - β cta )
Avec β = v/c, et le facteur de Lorentz γ :
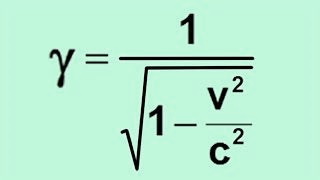
On se doute bien que cela va avoir des conséquences sur l'énergie, en particulier cinétique, vu qu'elle dépend directement de la vitesse (au carré). Et la masse ?
Masse et poids
Le principe fondamental de la dynamique relie la somme des forces à dérivée de la quantité de mouvement, qui est le produit de la masse par la vitesse :
A l'école, on nous apprend que la dérivée de la vitesse, c'est l'accélération, autrement dit la force est le produit de la masse, constante, et de l'accélération.
L'attraction gravitationnelle entre deux masses est une force qui tend à les rapprocher, et qui vaut :
d est la distance entre les deux masses, et G la constante gravitationnelle qui ne dépend que du système d'unité utilisé, en l'occurrence G vaut 6,67× 10−11 N m²/kg²
En considérant la masse de la Terre estimée à 5,972×1024 kg et son rayon de 6371 km, cela donne l'accélération de la pesanteur g, qui relie la masse et le poids : 9,81. Un kilogramme-force vaut 9,81 Newton, c'est la force qui s'exerce sur une masse d'un kilogramme.
Equivalence masse-énergie
Avec γ comme défini auparavant :
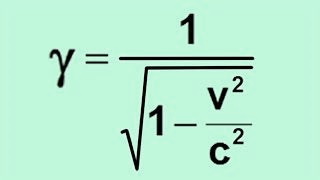

A présent, un exemple peu courant de conversion énergie-masse, ça changera des centrales nucléaires.
Deux trous noirs en collision
Nous allons se faire percuter de plein fouet deux trous noirs à des vitesses relativistes. Pour se simplifier la vie, nous allons supposer qu'ils iront à la vitesse de 0,8c (β=4/5 et γ=5/3), et on observe tout ça de loin. On négligera la gravitation, vu la vitesse, on n'est pas à ça près et ce n'est pas le point.
Deux trous noirs identiques
Pour commencer, nous allons considérer deux trous noirs de la même masse, une masse solaire. Prenez Beltegeuse si vous trouvez que notre soleil est petit joueur.

La quantité de mouvement (relativiste) γ m v vaut :
Positive pour l'un, négative pour l'autre, le total est, bien sûr, nul.
L'énergie cinétique (relativiste) de chaque trou noir ½ γ m v² vaut :
Au total, le double. On remarquera que l'énergie cinétique est évidemment énorme, de l'ordre de grandeur de la masse des trous noirs...
Percussion
Lorsqu'ils se percutent en collision frontale (ce qui est différent du cas des 2 trous noirs qui orbitent l'un autour de l'autre) il se produit une collision totalement inélastique et très soudaine, vues les vitesses. Rien ne ressort d'un trou noir, une coalescence se produit et c'est tout, rien n'apparait en dehors de l'horizon des évènements, cela n'aura rien à voir avec deux boules de billard... Le résultat sera un trou noir (sauf très grosse surprise physique).
Mais bon, avec ces vitesses, on peut raisonnablement se demander quelle va être la tronche de la fusion des deux horizons des évènements juste au moment de la percussion : ovale ? Ce serait logique. Le cœur ne va quand même pas rester bien symétrique, sphérique...
Pour le coup, il est probable que cela se verra de l'extérieur, la lumière autour du trou noir apparaitra déformée momentanément.
Et que va devenir l'énergie cinétique ? Avec deux voitures, les carrosseries se déforment pour l'absorber. Mais là ? L'énergie cinétique se transforme en quoi ? Je vous le demande ! En ondes gravitationnelles ? Est-ce que des ondes gravitationnelles peuvent s'échapper de l'horizon des évènements ? A priori non, sinon il va falloir revoir notre copie concernant la relativité générale.
Arrêt total
Comme la situation est parfaitement symétrique, le résultat est très prédictible : un trou noir, somme des deux trous noirs, se forme et reste sur place avec une vitesse nulle, vu que la quantité de mouvement est nulle.
Et la totalité de l'énergie cinétique se retrouve incluse dans le trou noir résultant, par simple conservation de l'énergie, au total :
Comme je ne vois pas quoi d'autre pourrait arriver (on ne connait rien de la structure interne d'un trou noir sauf que c'est très compact), toute l'énergie cinétique est convertie directement en masse :
Par quel mécanisme physique se produit la conversion énergie cinétique vers la matière ? Bonne question ! La matière au cœur d'un trou noir est tellement dense qu'on ne connait pas ses propriétés, et on ne risque pas de les connaitre vu qu'aucun signal ne sort d'un trou noir. Toutes les spéculations sont possibles.
Deux trous noirs de masses différentes
Pour avoir une situation moins symétrique, un des deux trous noirs aura une masse double, soit 2 masses solaires ☉+☉
La vitesse reste la même, 0,8c soit β=4/5 et γ=5/3.
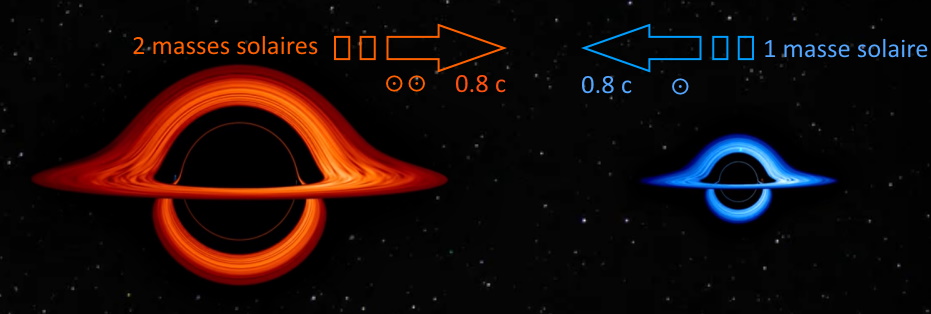
La quantité de mouvement (relativiste) γ m v vaut :
-γ β c ☉ = - 4/3 ☉ c
L'énergie cinétique (relativiste) ½ γ m v² vaut :
½ γ β² c² ☉ = 8/15 ☉ c²
La totalité de l'énergie cinétique équivaut à 8/5 ☉.
Vitesse du trou noir résultant
Il est à peu près évident que le premier trou noir, deux fois plus gros, l'emporte, et le trou noir résultant continue sur la trajectoire du premier. On peut alors se poser la question de sa vitesse vf.
On connait sa quantité de mouvement, qui est la somme des deux quantités de mouvement initiales :
Et là, on aimerait bien remonter à la vitesse, sauf que l'on ne connait pas la masse finale. Classiquement, on s'en sort en utilisant la conservation de l'énergie cinétique. Mais là, ça ne marche pas, car on ne sait pas quelle fraction d'énergie cinétique est convertie en masse, on n'est plus dans le cas précédent où on n'avait aucun choix !
On va utiliser la conservation de l'énergie totale :
Oui, j'ai mis directement des valeurs numériques, c'est plus facile pour voir ce qui se passe.
On introduit une inconnue, une masse x supplémentaire qui apparait (ou disparait), mf = (3+x)☉, ce qui donne :
En introduisant βf = vf / c, on simplifie :
Nous avons alors deux équations (énergie et quantité de mouvement) :
(3+x) γf βf = 4/3
La résolution (numérique) de l'équation donne le résultat :
Autrement dit, un phénomène physique particulier lors de l'impact impose de transformer exactement 0.353 ☉ c² d'énergie cinétique en masse, et le trou noir résultant aura ralenti à la vitesse de 0.369c au lieu de 0.8c auparavant. Mais quel phénomène ?
Voilà un joli problème ouvert, comme on dit quand on ne sait pas répondre.