Relativité

La théorie de la relativité restreinte (special relativity en anglais) concerne les repères dits galiléens, en fait nos repères habituels, où on fait abstraction de mouvements bizarres comme des rotations, et qui ne sont pas perturbés par la gravitation (sinon il faut considérer la relativité générale).

Comme nous n'avons pas repère absolu universel d'espace et de temps, inutile d'essayer de considérer un seul repère, c'est TOUJOURS au moins deux repères qui sont concernés.

Et pour que ça devienne intéressant, on aura toujours un mouvement de translation rectiligne uniforme entre les deux repères, à une fraction de la vitesse de la lumière, vitesse indépassable en l'état actuel de nos connaissances.

J'utiliserai pratiquement systématiquement deux personnages, Alice et Bob, chacun dans leur repère propre. Notez l'utilisation du mot propre : le temps propre d'Alice est ce qu'indiquerait une horloge atomique accrochée à son cou. Alice sera souvent dans une station spatiale, éloignée de tout, et Bob dans un vaisseau spatial, mais c'est un choix arbitraire, on observera uniquement qu'ils ont une vitesse relative v, et je choisirai souvent 80% de la vitesse de la lumière pour fixer les idées.

La théorie de la relativité restreinte permet à Alice de calculer ce qui passe pour Bob sur les aspects spatio-temporels = pour le temps et les longueurs. Autrement dit, elle donne les formules de changement de référentiel, que voici :

Transformation de Lorentz pour passer du référentiel Alice (x_a,t_a) au référentiel Bob (x_b,t_b) se déplaçant à la vitesse v le long de l'axe des x, et c la vitesse de la lumière :

│ ct_b = γ ( ct_a - β x_a )
│  x_b = γ (  x_a - β ct_a )
│  y_b = y_a
│  z_b = z_a

Avec β = v/c, et le facteur de Lorentz γ :

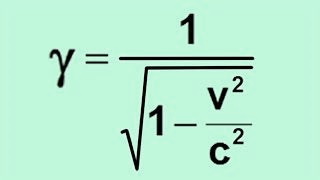
On oubliera les y et z qui sont inchangés.

Et réciproquement :

│ ct_a = γ ( ct_b + β x_b )
│  x_a = γ (  x_b + β ct_b )

Notez le changement de signe, qui indique que la vitesse est inversée.

Les coordonnées (x_a,t_a) ou (x_a,ct_a) s'appellent un évènement dans le repère considéré (je n'ai pas mis y et z par fainéantise).

Dans notre exemple, la vitesse v de Bob vaut 80% de la vitesse de la lumière c, on a :

des valeurs de feignasses, pratiques pour calculer.

On peut facilement se vautrer en utilisant la transformée de Lorentz un peu vite et confusément. Pour éviter ça, il faut systématiquement manipuler des évènements, autrement dit un jeu de coordonnées spatio-temporelles (x,t) (ou (x,y,z,ct) pour les puristes).

Pour mesurer un objet, il nous faudra deux évènements, un évènement à chaque bout de l'objet.

Pour faire simple, Alice choisit pour le premier évènement E0 (0,0), et pour le second E2 (t_a,x_a) en coordonnées d'Alice, x_a donnant la longueur de l'objet pour Alice.

Bob devra faire la même chose. Egalement pour faire simple, on force Bob à utiliser également l'évènement (0,0), puis le même second évènement E2 (t_b,x_b) en coordonnées de Bob.

Comme on a choisi E0 en (0,0), tout est à zéro, que ce soit pour Alice ou Bob, ce qui nous facilite la tâche. La transformation de Lorentz lie les coordonnées de l'évènement E2, et c'est plus astucieux d'utiliser la transformation inverse :

La mesure doit être faite au même instant que E0 par Bob, et donc t_b=0 :

La première équation est sans intérêt, elle donne l'heure de mesure pour Alice. La seconde équation nous donne la taille de l'objet pour Alice en fonction de la taille pour Bob.

Comme γ est toujours plus grand que 1, la longueur chez Bob n'est pas la même chez Alice, elle est plus courte, ce sont les histoires de contraction des longueurs.

Le rapport est donné par le facteur de Lorentz γ, c'est pour ça qu'il est si important. Le facteur de Lorentz γ est toujours supérieur à 1.

Voici un premier exemple bateau pour commencer à s'habituer.

Alice est sur la station Alpha. Il existe une seconde station spatiale, DS9, située à 20 années-lumière d'Alpha. On remarquera que les deux stations sont dans le même repère galiléen, celui où se situe Alice.

Bob est dans son vaisseau qui bourre à 80% de la vitesse lumière. Quel est la distance vue par Bob entre les deux stations spatiales ?

On vient de le voir juste avant, on observe une contraction des longueurs :

La longueur vue par Bob est de 20 * 3/5 = 12 a.l.

La transformation de Lorentz est en fait assez simple : elle permet que la loi de composition des vitesses, habituellement une simple addition, interdise de dépasser la vitesse de la lumière, et c'est pour ça que l'on voit cette vitesse maximale dans les formules.

Mais le concept est perturbant car on vient de voir que le temps se dilatait et l'espace se contractait quand Alice mesure ce qui se passe chez Bob. À la limite, pourquoi pas ? Mais c'est pareil pour Bob, il voit le temps d'Alice se dilater et son espace se contracter... 😖