Les ordinateurs quantiques
qubit: reboot

Dans le cas de la lumière polarisée, cela permet de décrire une onde diagonale comme étant la somme bête et méchante de deux ondes, une verticale et une horizontale mais si, vous savez déjà cela.

Mais il faudra que le déphasage entre les deux ondes soit nul. Si le déphasage est non nul, alors on aura des ondes elliptiques voire circulaires, qui tournent.

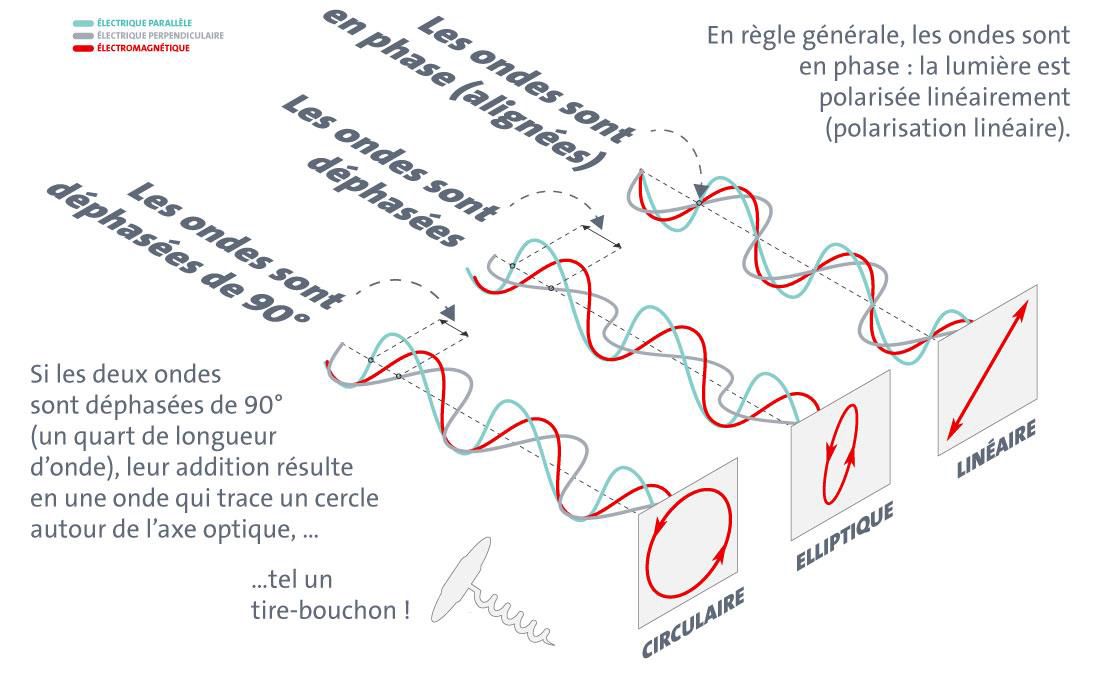
On peut donc alors décomposer n'importe quelle onde dans une base (orthonormée) : on choisit par exemple { horizontal |→⟩ , vertical |↑⟩ } Non mais c'est quoi cette notation ?

Eh bien les gars qui travaillent en mécanique quantique, ils écrivent leurs vecteurs avec la notation de Dirac, des "bra"-"ket" bra pour ⟨ et ket pour ⟩

Ce qui leur permet de se la péter et de se différencier du vulgaire matheux. .

Pour une onde diagonale (à 45°), on aura :

Vous noterez avec bonheur que nous avons une superposition, qui est ici une somme bête et méchante.

Mais vous noterez aussi :

• les amplitudes peuvent être différentes : l'angle de polarisation ne sera plus exactement diagonal
• il peut aussi exister un déphasage : l'onde sera elliptique / circulaire.

La fréquence f est la même dans les deux termes, bien sûr.

Deux autres paramètres sont requis pour chaque terme, autrement dit pour chaque vecteur de la base : l'amplitude et la phase. Ceci dit, seule la différence de phase compte, aussi on n'a en réalité que 3 paramètres indépendants.

Le module n'est jamais que l'amplitude de l'onde et on applique Pythagore pour le calculer (le carré de l'amplitude est la somme des carrés).

On peut aussi choisir une base diagonale -et on aime bien faire ça en cryptographie quantique, vous l'avez déjà vu avec les histoires de protocole BB84.

Au lieu d'utiliser des cosinus, on peut utiliser une notation complexe (avec des nombres complexes) Vous voyez, avec des nombres complexes, on rend les choses plus simple.

C'est quand même curieux 😋 grâce à la formule d'Euler : e ^{i Φ} = cosΦ + i sinΦ

Et c'est comme ça qu'on arrive gentiment à la notation de Dirac, avec deux nombres complexes :

Et on retrouve dans chaque nombre complexe α et β l'amplitude et la phase, phase qui traine dans la partie imaginaire.

Le carré de l'amplitude est proportionnel à l'énergie de l'onde électromagnétique. Rien de spécial de ce côté-là à part le fait que l'on sait que si une interaction se produit avec une particule, par exemple avec l'électron d'un atome, alors l'échange d'énergie est quantifié : ce n'est pas n'importe quelle onde électromagnétique qui va réagir avec tel électron dans telle condition.

Typiquement, l'énergie

où ℎ est la constante de Planck, f la fréquence et n entier évidemment, sinon, c'est con. L'énergie est quantifiée, donc l'amplitude est aussi quantifiée. C'est pour ça qu'on préfère parler de photon, ça fait particule.

Par exemple, pour un photon diagonal, la moitié de l'énergie sur le côté horizontal et l'autre moitié sur le côté vertical, cela ferait une amplitude de √½ dans le monde classique.

Et on ajoute la propriété dite condition de normalisation:

Autrement dit, sa norme est 1, le vecteur est toujours de longueur 1. Logique, c'est une probabilité: on trouvera le photon à coup sûr d'un côté ou de l'autre. Ici, le carré de 1/√2 vaut ½, donc 50% de chance d'obtenir un photon vertical. Et pareil pour un photon horizontal, dans ce cas particulier.

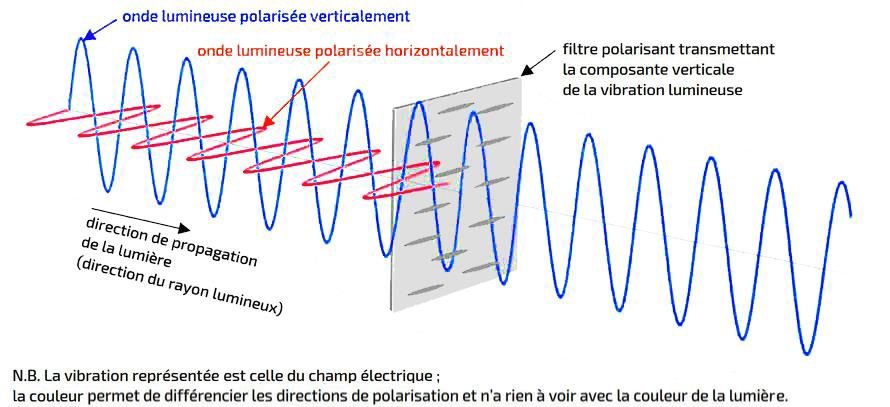
Rappelez-vous du détecteur de photon :

Nous avons une source de photon unique, puis un détecteur de photon : c'est la mesure. On compte les photons un par un pendant un certain temps.

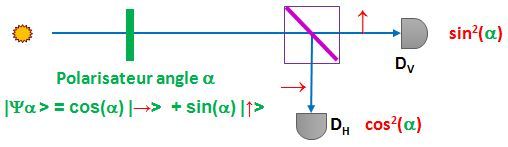
En faisant passer notre lumière dans un polarisateur présentant un angle de polarisation α , on a :

Juste avant, l'angle α valait 45°, et donc les deux coefficients valaient 1/√2. On notera que le carré de la norme vaut cos² + sin², dont le résultat est évidemment 1 si vous vous rappelez un peu votre trigonométrie. Ça tombe bien, vu qu'il faut que ce soit 1, c'est la probabilité totale de détection.

Ajoutons un cube polarisateur qui transmet tout droit une polarisation verticale et dévie une polarisation horizontale, c'est son job (et c'est notre base orthonormée). L'angle α est l'angle que fait l'axe du polarisateur avec l'axe du cube de polarisation c'est là que c'est malin d'utiliser la base orthonormée correspondant au cube :

La lumière a été filtrée par le polarisateur avec un angle α . Toute la lumière est à présent polarisée rectilignement avec cet angle. Ensuite, le cube de polarisation a filtré la composante verticale pour aller d'un côté, et la composante horizontale restante est allée de l'autre côté. Côté intensité lumineuse, on a :

• sin²(α) du côté vertical (l'amplitude au carré)
• cos²(α) pour le côté horizontal.

C'est la loi de Malus, connue depuis des lustres en optique.

Pas question de diviser le photon en plusieurs morceaux !

Cette fois, on parle de probabilité. La probabilité d'avoir un photon

• en polarisation verticale est le carré de la valeur du coefficient devant |→⟩ soit sin²(α)
• et celle en polarisation horizontale l'autre coefficient au carré, cos²(α)

On parle alors de superposition car le photon est soit l'un, soit l'autre, mais pas les deux.

Dans le cas particulier où le photon est polarisé diagonalement (avec un angle de 45°), alors on observera une détection la moitié du temps côté horizontal, et vertical sinon.