
Ainsi vous avez vu au moins une des deux démonstrations montrant que l'espace et le temps sont distordus lorsque l'on regarde les autres se déplacer.
Cette relativité est très symétrique. Lorsque qu'Alice et Bob se rejoignent, lequel a sa pendule qui avance ? Lequel a sa règle qui déconne ?
Transformation de Lorentz
Nous avons vu que l'espace et le temps ne sont plus les mêmes dans un référentiel galiléen en déplacement par rapport à nous.
Ce sont les mathématiciens qui ont trouvé les formules qui mettent en relation le temps et l'espace entre deux référentiels en déplacement relatif à vitesse constante.
Les déformations sont linéaires (ouf !) : un facteur habituellement nommé γ (gamma) qui dépend du ratio β (beta) de la vitesse sur la vitesse de la lumière, indique le rapport de distorsion.
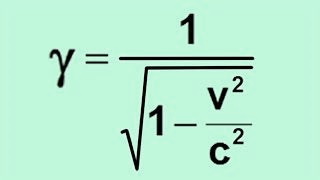
γ vaut pratiquement 1 dans le cas des faibles vitesses, et on revient alors au cas newtonien, mais peut prendre des valeurs énormes lorsque l'on s'approche de la vitesse de la lumière, ce qui est difficile à faire car il faut une énergie extraordinaire pour y arriver.
Temps propre et impropre
Comme le temps ne s'écoule pas de la même manière dans les différents référentiels, il a fallu distinguer le temps qui s'écoule où vous êtes, et le temps "ailleurs".
- Le temps propre est le temps qui s'écoule pour vous. Vous pouvez vous le représenter comme étant une horloge atomique accrochée à votre cou, c'est votre temps.
- Sinon, c'est un temps impropre.
Dans le cas de deux référentiels, c'est facile à désigner, mais dès que vous êtes plus de deux, eh bien c'est la zone pour dénommer les différents temps, et vaut mieux utiliser une notation qui indique de quel référentiel on parle...
Symétrie
Vous avez certainement remarqué la symétrie de la situation :
- Alice voit le temps de Bob ralentir, et l'espace de Bob se contracter
- Mais la situation est identique du point de vue de Bob ! Le temps d'Alice ralentit, et son espace se contracte !
Cette symétrie apparente cause de nombreux maux de tête à pas mal de gens, à commencer par nous. Ce sont des discussions qui paraissent sans fin, en particulier dans le cas du paradoxe des jumeaux de Langevin, alors que c'est en fait très simple si on applique bien quelques éléments basiques.
Nous allons faire exprès de garder la symétrie aussi longtemps que possible pour vous montrer où, à quel moment il faut appliquer une remarque pertinente qui cassera cette symétrie.
Notez quand même, en considérant plusieurs repères, que :
- Le temps s'écoule le plus rapidement dans un repère fixe (là où vous êtes). Chez tous les autres, le temps s'écoule plus lentement.
- Les distances sont toujours les plus longues dans un repère fixe (là où vous êtes). Chez tous les autres, les distances se contractent.
Mais cette remarque, importante, est manifestement insuffisante pour convaincre les personnes empêtrées dans la symétrie.
Alice et Bob pensent que c'est l'autre
Prenons un exemple canonique avec deux référentiels qui se croisent à 80% de la vitesse de la lumière, l'un avec Alice et l'autre avec Bob. Ils se croisent lors de l'évènement zéro, par convention et par facilité, le temps démarrera à zéro à ce moment-là :

À 80% de la vitesse-lumière, on parcourt 20 minutes-lumière en 25 minutes, ou 20 années-lumière en 25 ans, choisissez ce que vous voulez. Ici on va prendre des minutes car cela laisse l'impression que la réunion sera plus facile, mais en fait ça ne change rien.

Vous voyez que l'on a fait exprès de déplacer les deux zouaves sur le dessin, mais c'est juste votre cerveau qui fait le troisième observateur et qui complique implicitement les choses. Alice s'éloigne de Bob à 80% de la vitesse de la lumière, Bob s'éloigne d'Alice à 80% de la vitesse de la lumière.
Contradiction ?
À cette vitesse relative, le γ vaut 1.666.
Alice voit le temps de Bob ralentir, autrement dit l'horloge d'Alice indique 25 minutes, et celle de Bob doit indiquer 15 minutes.
Et c'est pareil pour Bob ! L'horloge de Bob indique 25 minutes, et celle d'Alice doit indiquer 15 minutes.

Réunification

Attention, c'est là que ça se joue.
Une dissymétrie est en train d'être introduite !
Dans ce cas, il faut utiliser la transformation de Lorentz où Alice est fixe, c'est la référence. C'est Bob qui change de vitesse, c'est lui qui modifie son état. Les équations sont claires : le temps ralentit chez les autres.

L'expérience de Hafele-Keating l'a effectivement constaté à l'aide d'horloges atomiques voyageant dans un avion.
Et rappelez-vous qu'un accéléromètre permettra de savoir celui qui a pris de la vitesse, par rapport au sédentaire.
Cette histoire sera encore détaillée lors de l'analyse du paradoxe des jumeaux.
Échange ?
Il existe une situation intermédiaire symétrique facile à comprendre.
C'est lorsque Alice accélère et Bob freine de manière à arriver dans le référentiel "milieu". Dans ce cas, ils ont le même âge, évidemment, par symétrie. Ils ont tous les deux changés de vitesse, aucun n'est fixe.
Age paradoxal
Un autre cas rigolo et paradoxal est le départ de deux Bob à exactement la même vitesse par rapport à Alice.
- S'ils ont des trajets parallèles, il est évident que les deux Bob auront le même âge, leur vitesse relative est nulle.

- Mais s'ils ont des trajets perpendiculaires, ou carrément opposés, les deux présenteront une vitesse relative non nulle. Et pourtant, lorsqu'ils freineront pour retrouver le référentiel d'Alice, ils auront quand même le même âge...

C'est d'ailleurs vrai quelle que soit leur direction relative.


Les distances sont conservées,
pas le temps
Puisqu'une accélération modifie la vitesse, ce qui provoque des distorsions spatio-temporelles, on peut alors se demander quel est l'effet de la gravitation, qui applique une force donc une accélération, dans l'univers.
C'est la généralisation de la relativité restreinte, appelée relativité générale.
